Thermodynamics of Solutions - First Year, Trinity Term (4 lectures)

Behaviour of Ideal Solutions

Vapour Pressure of a Solvent above a Solution (Raoult's Law)

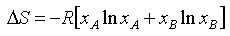
An ideal solution may be defined as one for which the entropy of mixing is given by equation (E2), i.e.

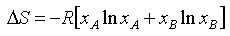
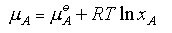
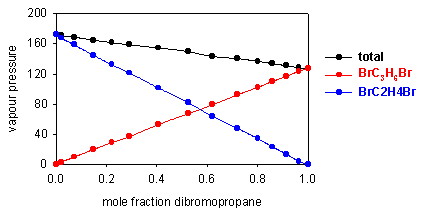
and the enthalpy of mixing is zero. The most convenient definition, however, combines these into the single equation (M1) for the chemical potential, i.e.

We use the second equation, or a related form, to derive all the equations describing the physical properties of ideal solutions. Although the ideal solution model is often only a rough approximation for the true behaviour, it serves as a very useful reference point for discussing actual behaviour. We start with Raoult's Law, which describes the vapour pressure of a solvent (A) above one of its solutions.

Raoult's Law requires the vapour pressure of the solvent to vary linearly with its mole fraction in the solution. Such truly ideal behaviour is rare; the two components of the mixture have to be very similar. An example is shown below for a mixture of dibromoethane and dibromopropane. Each component obeys Raoult's Law over the whole concentration range.

Two further examples are shown below, one (acetone/chloroform at 36oC) showing a negative deviation from Raoult's Law (vapour pressure higher than ideal) and the other (acetone/CS2 at 50oC) a positive deviation. For these two systems Raoult's Law is only obeyed by the solvent when the concentration of solute is small (regions looped with green). The vapour pressure of the solute deviates very considerably from Raoult's Law at low concentrations of solute (regions looped with magenta).

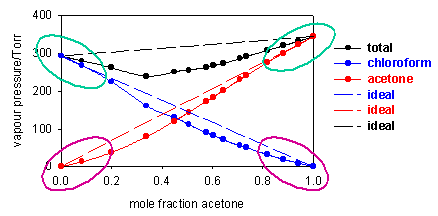
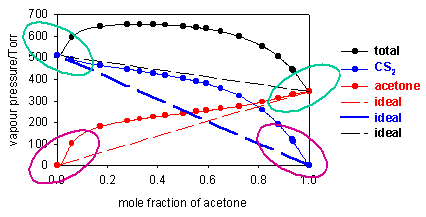
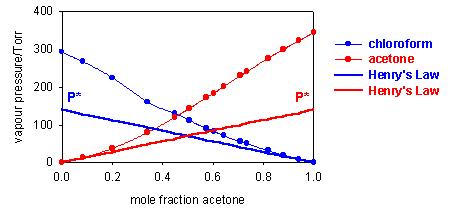
Vapour Pressure of a Solute above a Solution (Henry's Law)

Although Raoult's Law does not at all account for the vapour pressure of the solute at low concentrations, the diagrams above indicate that in these regions the vapour pressure is nevertheless proportional to the mole fraction of solute, i.e. we can write

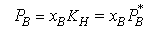
The question is then how to reconcile this empirical behaviour with the ideal solution model. The panel below shows that if, in our basic equation for the chemical potential, we replace the chemical potential of the pure substance with an empirical value, we can account for the linear behaviour of the solute vapour pressure. This relationship is called Henry's Law.

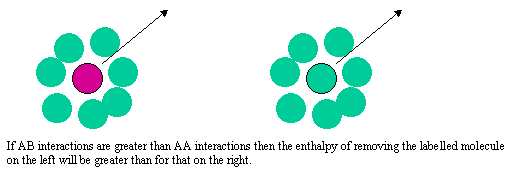
The difference between the two types of behaviour can be explained quite simply by considering what determines the chemical potential as the mole fraction of either A or B tends to zero. The two limiting situations are shown in the diagram below. In Henry's Law the solute molecule is surrounded by solvent molecules at the limit. In Raoult's Law the solvent molecule is surrounded by other solvent molecules. If the enthalpy of the AB interaction is greater than for AA and BB the chemical potential of a solute molecule B surrounded by solvent molecules A (Henry's Law) will be lower than when it is surrounded by B molecules (Raoult's Law).

Partition of a Solute between two Immiscible Liquids

When a solid such as iodine is shaken to equilibrium with two immiscible solvents such as toluene and water it will partition between them. At low iodine concentrations an iodine molecule will be surrounded by water molecules in the one solution and toluene in the other. This will almost certainly lead to a difference in the chemical potential of the iodine in the two situations and this should determine the relative solubilities in the two liquids. As shown in the panel below ideal solution behaviour indicates that the ratio of the two solubilities should be independent of overall concentration.

Equation (P) offers a straightforward means for determining equilibrium constants that would otherwise be somewhat inaccessible. The equilibrium between I2, I- and I3- in aqueous solution is not easy to measure because during titration to determine the amount of I2 the I3- reverts rapidly back to I2 and I-. If toluene is added and the aqueous/toluene mixture equilibrated then separate titrations on the toluene and aqueous layers give [I2](toluene) and ([I2] + [I3-])(water) respectively. Since the partition coefficient is known (determined in a separate experiment) the true aqueous [I2] can be determined and hence [I3-](aqueous) by subtraction.