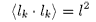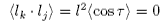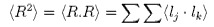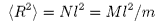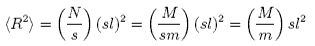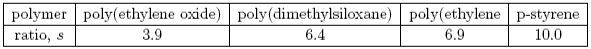(i) Set the density to its maximum value and press the reset button. This shows the regular lattice used as the starting point. Start the simulation and convince yourself that there is no temperature at which this solid will melt. Although the vibrational motion in the lattice becomes more vigorous at the highest temperature, the regularity of the lattice structure is maintained. This is best monitored by choosing to look at the radial distribution function. At all temperatures it consists of discrete peaks, as described in the introduction, although the peaks do broaden as the temperature increases.for the calculation.
(ii) With the simulation still running, gradually decrease the density until the solid melts (note that density changes on the display are shown by scaling the atom size to a changing box size). You can monitor melting in part through the radial distribution function and in part by watching one atom and seeing when it is displaced from one "lattice position" to another. Play around with different combinations of temperature and density. The liquid state is distinguished by the atoms becoming delocalised (they will in time sample the whole space) and by the radial distribution function being non-zero at all points greater than the core radius.Unfortunately the size of the box is not large enough to see the convergence of g(r) to unity.
(iii) Lower the density to its minimum value and gently increase the temperature to its maximum value (gently, because a sudden change in time step and energy may generate a configuration where the cores of two atoms overlap and then the energy of the system jumps to unmanageable values; if this happens, just press reset). You will now see typical gas phase motion of the atoms, although the density is a lot higher than a typical gas. The radial distribution function under these conditions is as described in the introduction. There is an exclusion zone corresponding to the hard cores and a slight maximum at distances beyond this where the attraction between the molecules causes them to undergo sticky collisions.
(iv) With the density at its minimum lower the temperature and you will see that the atoms start to form small clusters (this takes some time). On the limited scale of the simulation this is condensation to form drops of liquid. It makes it clear that the attractive forces are responsible for the formation of the liquid state. These clusters would not form if the potential were purely repulsive.
(v) Finally reexamine the transition between solid and liquid, convincing yourself that the attractive forces only play a very minor role in this transition, which can be approximately described as occurring when the vibrational amplitude is large enough to displace an atom from one lattice position to the adjacent one.
A qualitative feel for some of the main issues to do with mixing can be obtained from the quantitative model shown below. This is a Monte Carlo simulation of a 2D version of something called the Ising model.
The applet allows you to do your own simulations. It demonstrates mixing on a lattice and, although the model is derived from a model to describe magnetic interactions, the mathematics is appropriate to the mixing of two liquids. Some suggestions for simulations are outlined below the diagram.
As set up here the program simulates the mixing and demixing of two liquids A and B on a square lattice. There are two adjustable parameters, the temperature and an interaction parameter, which is a measure of the interaction energy between A and B. The starting lattice configuration can be chosen to be either the separated liquids A and B or the perfectly ordered mixture. The former corresponds to the low temperature limit of strong repulsion between A and B and the latter to the low temperature limit of strong attraction between them. You can switch between the different starting points by toggling the Reset Button. The method used for the simulation is the Monte Carlo method, which is completely different from that used for the simulation shown in the section on the Radial Distribution Function. The following section in italics, which you do not need to understand, outlines the method. The subsequent paragraph suggests some simulations that you might perform.
An equal number of A and B "atoms" is displayed initially on a square lattice, each atom having four nearest neighbours. One of these, chosen at random, has its identity reversed (B becomes A or vice versa). The resulting change in energy and the corresponding Boltzmann factor (exp(−ΔE/RT)) are computed. If the Boltzmann factor is greater than a random number between 0 and 1 the change is accepted, if not it is rejected (i.e. decreases in energy are automatically accepted, increases in energy are accepted with decreasing probability as they become larger). The procedure is then repeated as long as required. The weighting of the choice of configurations towards those that are energetically more favourable ensures that the system reaches equilibrium much more efficiently than would be achieved with purely random changes. The method is known as the Monte Carlo method, it is exceedingly widely used for the solution of problems of this type, and the code used here can be found in Chandler: Introduction to Modern Statistical Mechanics, Oxford, 1987, pp 184-5. Note that periodic boundary conditions are used, as in the simulation shown earlier, to minimize the effects of the boundaries. It may seem from the operation of the program here that multiple changes are being implemented. This is not the case but, since the display is the slow part of the simulation, it is only being updated after every 20 successful moves.
The following are suggestions for some basic simulations.
(i) Before starting the program, set the B slider to 0. This corresponds to zero interaction between A and B, i/e/ to an "ideal" system. Start the program. The system very rapidly mixes, i.e. at the minimum temperature of 150 K the system will mix. Note that this occurs even though there is no net interaction between A and B. The interactions AA, BB and BB are all equal. This is ideal mixing. What would be the differences in the radial distribution functions gAA, gBB and gAB?
(ii) Reset the system to start with the separate A and B phases and start the simulation keeping both sliders in their initial positions (lowest temperature and maximum attraction) and confirm that the system equilibrates to the "chessboard" configuration as expected. When the system seems reasonably stable change the interaction parameter to zero and allow the simulation to run for a while. Note that the appearance is not the same as with B = -2000 J mol−1. Increase the interaction parameter to +2000 J mol−1 and, again, allow the simulation to run for a while. What happens? Note also how it happens. The large clusters grow at the expense of the small clusters. Now increase the temperature to its maximum value and again wait to see what happens.
(iii) Repeat the above but starting from the initial chessboard or mixed congiguration using the reset button.
(v) Start the simulation from the phase separated condition with the energy set to maximum repulsion, i.e. slider to the right, but at the lowest temperature. The system remains phase separated, although there are significant fluctuations at the two interfaces. Increase the temperature gradually and observe the amplitude of these fluctuations increase. Can you suggest a reason for the fluctuations? Continue to increase the temperature and estimate the point at which mixing is complete. Then decrease the temperature and test the extent to which you can reverse the process. The phase separation is reversible but it is difficult (not impossible) to recover the initial positioning of the to separated phases. If you try this you will find that it is the periodic boundary conditions that are the main obstacle. Download simulation.jar with SimulationApplet.html for the simulation (or better still download the original). Download the ising program and the Ising control program if you want to use these separately.
The applet (adjustable diagram) shows how the vapour pressures of solvent and solute behave in a mixture ( Click here for notes about the use of java applets and click here for other physical chemistry applets). The diagram deals with the vapour pressures of ideal and regular solutions and can illustrate a wide range of situation. In an ideal solution there is no interaction and hence ideal behaviour is obtained by setting the Interaction Parameter to zero. When you do this you will see that the enthalpy of mixing is zero (left hand graph). TΔS and ΔG are also shown on the left hand side. When ΔH is zero the vapour pressures on the right hand side coincide with the ideal (black) values and conform to Raoult's Law over the whole composition range. Only for very similar pairs of liquids, e.g.dibromoethane and dibromopropane, is Raoult's Law obeyed over the whole range of mole fraction. In the common situation where it is not obeyed there are two types of behaviour, positive deviations, e.g. carbon disulphide and propanone, and negative deviations, e.g. trichloromethane and propanone. In these examples Raoult's Law is only obeyed where the solute concentration is low.
The standard examples showing (a) a strong positive deviation from Raoult's Law is acetone/carbon disulphide and (b)showing a stong negative deviation is acetone/chloroform. In the former the strong dispersion forces between the very polarizable sulphur atoms dominate and in the latter a weak hydrogen bond forms between the carbonyl group of acetone and the CH bond of chloroform. When the interaction parameter β becomes sufficiently large and positive A and B will demix. The regular solution model can be used to predict the pattern of the phase separation of the two partially miscible components.
A quantitative model of the miscibility of two liquids is illustrated in the applet below. On the right is shown the phase diagram of two partially miscible liquids calulated according to the regular solution model. On the left are shown the three thermodynamic parameters. If the interaction parameter has a small positive value, the entropy of mixing ensures that the two liquids mix in more or less all proportions. As the interaction parameter increases so the entropy of mixing is less able to dominate the positive enthalpy of mixing and the free energy of mixing, although remaining negative overall, acquires a shape with two minima and one maximum. In the region between the two minima the free energy of the system is lowest if the system remains as two immiscible solutions with compositions corresponding to the two minima. This is because the free energy of such a phase separated system is represented by a horizontal line tangential to the two minima, whereas the free energy of the fully mixed system would follow the double minimum curve. The compositions of the two immiscible solutions are easily determined by finding the two minima in the free energy of mixing. This method has been used to calculate the phase diagram on the right hand side of the diagram below. As can be tested from the diagram the phase separation region widens as the interaction parameter becomes more repulsive and raising the temperature narrows it. There are some further points of interest. The dynamics of phases separation are driven by fluctuations. In general, if a fluctuation leads to a decrease in the free energy, it will happen spontaneously.In the diagram below there is a region coloured in pink where the variation of ΔG with a composition fluctuation is positive (examine the curvature of ΔG on the left hand side of the diagram). Spontaneous fluctuations in this region do not lead to phase separation. This makes the system metastable. The outer curve on the left then represents the true thermodynamic separation point and the inner curve, called the spinodal represents the end of the metastable region.
The compositions of the two phases in equilibrium in the above diagram and the value of the upper consolute temperature (the temperature at which the two solutions just become miscible) can be obtained by examining the properties of the differentials of the free energy of mixing. The compositions of the two immiscible phases are those corresponding to the two minima in ΔG, i.e. where the first derivative is zero and the second derivative is positive. The consolute temperature occurs at a point where both the first and second derivatives are zero, i.e. the plot has no curvature.
The regular Gibbs free energy of mixing is
Differentiating with respect to xA
This has two minima corresponding to the two immiscible phases in equilibrium and it has maximum at xA = 1/2. The equation for the minima cannot be solved analytically. However, further differentiation gives
This can be solved to give the upper consolute temperature as
The simplest model of a polymer structure is the three dimensional random walk (random flight; the next section describes this in detail). The applet below ( click here for notes about the use of java applets and click here for other physical chemistry applets; for downloading the relevant filename for the polymer applet below is randWalk.jar and the code to operate it is given at the end of this document) calculates a new one thousand step random walk each time the button is pressed. The end to end distance is given together with its cumulative average.
The polymer consists, at start-up, of 1000 segments of length unity and these are free to rotate through any angle with respect to adjacent segments (random flight model, three dimensional random walk model). The polymer is drawn in perspective to capture the 3-D structure. The two ends of the polymer are marked with black rings. The brighter coloured, larger segments are in the foreground and the paler, smaller segments are furthest away. On pressing New random walk a new configuration is generated. The right hand side shows the square root of the end-to-end distance of the configuration shown and the accumulated root mean square end-to-end distance. It also plots a histogram of the accumulated RMS end-to-end distances. There is one adjustable parameter, which is discussed further below.
You should try the following.
(i) Repeat the calculation enought times to generate a reasonably stable histogram of RMS end-to-end distances. Note the very wide variety of possible configurations, the quite wide distribution of RMS end-to-end distances in the histogram, and the large number of 'data' you have to accumulate to generate a representative distribution. Note also that there is a most probable RMS end-to-end distance and that this is the square root of the fully extended length of the polymer, i.e. 10001/2. Since this end-to-end distance is the most probable, it is the one for which the entropy has its highest value.
(ii) The lever changes the polymer as follows. It incorporates a number of the initial segments into a single segment (changes the persistence length) and correspondingly reduces the number of segments, thus increasing the length of an individual segment while keeping the fully extended length of the polymer constant. Set the value of the slider to a segment length of 2. Press restart to restrt the calculation of the histogram. You will notice that the values of the RMS end-to-end distance increase (the scales in the left hand graph have been kept as the original segment length of unity). Repeat the calculation until you have a representative histogram and compare the RMS end-to-end distances for segment lengths 1 and 2. The ratio should be 1.4 (21/2). The applet does the calculation numerically but the RMS end-to-end distance can also be related to the molecular weight and the length of the individual segments analytically as described below. The random flight model only seems unrealistic if one makes the mistake of assuming that a random flight segment is the same as a chemical segment. For each homopolymer the number of chemical segments needed to produce a segment that follows the random flight model varies according to the stiffness of the structure. This is essentially the calculation (ii) that you made for the applet above. The freely jointed chain consists of segments (not necessarily the chemical
segments) attached in such a way that each segment may take up any
orientation, with equal probability, with respect to its nearest neighbour,
i.e. if lk is a vector representing segment k then
and
for all values of j ≠ k and where τ is the angle between segments
k and j. A possible measure of the dimensions of the polymer is the end to end distance,
R. The problem is exactly the same as a random walk. After a
large number of steps the walker on average ends up exactly where he
started, i.e. <R> = 0. This is because
negative (backward) steps are as likely as positive (forward) ones.
However, the mean square distance,<R2>, is not zero and
that is what we take to characterize the chain length.
Thus
where N is the total number of segments, M is the molecular weight, and
m is the segment molecular weight. The important result is that the root
mean square end to end distance is proportional to the square root of the
molecular weight as shown in the applet above.
The random flight molecule is obviously unrealistic in that adjacent chemical segments cannot rotate freely. However, it is reasonable to divide the chain into sequences of chemical segments that are sufficiently long that these sequences obey the random flight molecule. If there are s chemical segments of molecular weight m in such a sequence the following result is obtained
The value of s is then a measure of the rigidity of the polymer. Some values are given below.
Radial Distribution Functions and Mixtures
Phase Separation and the Regular Solution Model
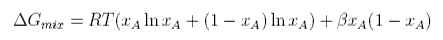
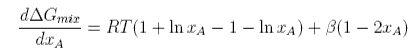
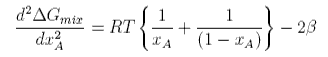
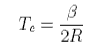
Dimensions of a Polymer Molecule