Liquids and Solutions, 2nd Year

Scattering Methods for Polymers and Surfactants

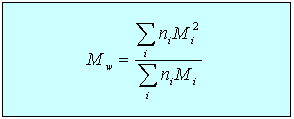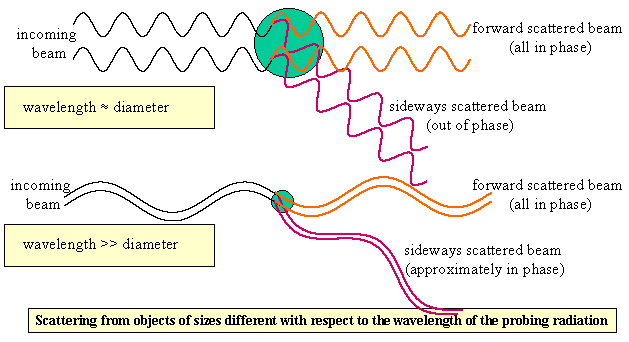
A full treatment of the scattering of radiation by an object of arbitrary shape is complicated but, for the purposes of determining the dimensions of a polymer or of a micelle, a relatively simple approach is effective. Taking a spherical object first, the radiation is the total of that scattered by each small element of the sphere. As shown in the figure, if the wavelength of the incident radiation is comparable with the size of the object there can be quite strong interference between the scattered waves from two parts of the sphere at larger scattering angles. If the object is small in comparison with the wavelength of the radiation, such interference becomes negligible (lower part of figure).

schematic diagram of scattering of radiation by an object small in comparison with the wavelength of the radiation

The diameters of micelles (aggregates formed by soap-like or detergent-like molecules in aqueous solution) are typically in the range 50 - 100 Å whereas the wavelength of visible light is 4000 -6000 Å. Light is therefore not very suitable for investigating micelle sizes. However, the shorter wavelengths of x-rays (typically 0.5 - 2 Å) and neutrons (typically 0.5 - 20 Å) make them both highly suitable for studying micelles. For these shorter wavelengths the two scattered waves in the figure would start in phase at zero scattering angle and then go out and in of phase as the scattering angle increases. For a perfectly spherical particle the scattering of x-rays and neutrons shows well defined interference features, from which the radius of the sphere can immediately be determined. This type of scattering is illustrated in the figure below. Both the amplitude and the intensity (squared amplitude) of the scattering are plotted as a function of a quantity k, which is defined in the figure and which depends on the angle of scatter (2q) and the wavelength of the incident radiation. The interference effects are highlighted by plotting log(intensity), as in the right hand graph. The calculations are exact for a sphere of radius 50 Å.

schematic diagram of scattering of radiation by an object comparable with the wavelength of the radiation

There are a number of systems where interference effects of this type can be seen with light. One is shown below for the light from the moon being scattered by small water droplets formed by condensation on a window pane. Because the light contains a band of wavelengths the interference effects are different for each wavelength and the pattern is therefore coloured.

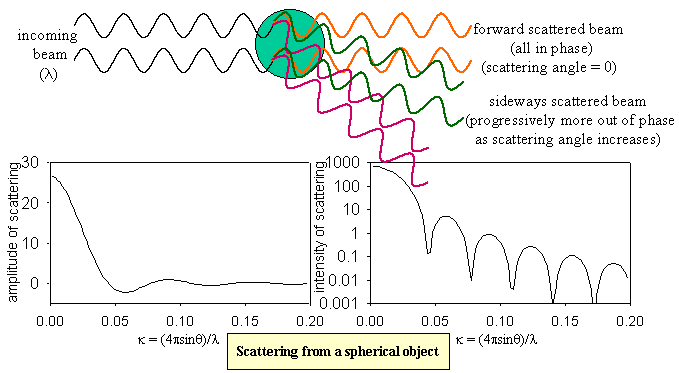
For polymer molecules the situation is not quite as simple. A polymer molecule in solution will have something close to a random flight configuration, and the details of the coil will be different for each molecule. The scattered intensity is now the square of the sum of the scattering from every segment in the molecule. In the limit where the polymer dimensions are very small in comparison with the wavelength of the radiation (typically, for light scattering, when M is less than about 106) the overall intensity is proportional to the molecular weight of the polymer. Light scattering is therefore a useful means of determining molecular weights. If the dimensions of the polymer are large enough relative to the wavelength of the incident radiation (which is always the case for x-rays and neutrons) there will also be interference of the scattered rays at higher angles (see figure below), from which information about the dimensions can be obtained. This is less regular than for the perfect sphere considered above and just leads to a general decay, following the equation:

lnI = lnI0 - k2Rg2/3

where k is as defined in the second figure above.

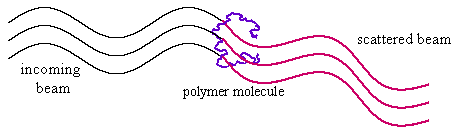
schematic diagram of scattering of radiation by a polymer

Using this equation it is relatively straightforward to determine the dimensions of a polymer in solution from the scattering behaviour of X-rays or neutrons. The scattering may be regarded as the average of the sum of the scattering from all pairs of segments in the polymer. This average is proportional to the radius of gyration, RG, of the polymer. Establishing a relation between RG and the root mean square end-to-end distance is not easy. In the case of a linear polymer of high molecular weight, RG = 61/2R0.

Light scattering may be used to determine the radius of gyration of larger polymers. When the light scattering is affected by the dimensions of the polymer and is also being used to determine the molecular weight it is necessary to extrapolate the scattering to zero scattering angle to obtain the correct molecular weight. Note also that, since the scattered intensity depends on the square of the scattered amplitude, higher molecular weight species in a polydisperse sample contribute more to the average than lower molecular weight species. Light scattering therefore gives the weight average molecular weight, Mw, whereas osmotic pressure gives the number average molecular weight, Mn. The ratio of the two is often given as an indication of the polydispersity of a sample.