Simple Solids and Diffraction

The two main characteristics of a solid are that it has long range order and that each atom is located in a particular position. The second property has the consequence that, unlike the vapour or liquid phases, the particles of a solid are "distinguishable". This is important in the statistical thermodynamics of solids. However, the issue here is that of the long range order, how to describe it and how to detect it.

Cubic Structures of Monatomic Systems

The structure of a solid is described as a combination of a lattice and a repeating unit. The lattice is generated by applying a set of symmetry operations to a point to generate an structure that fills space. Note that these symmetry operations are different from those with which you are already familiar for molecular point groups, which do not generate infinite lattices. However, like the molecular point group, there are only certain combinations of symmetry elements that generate the infinite structures. 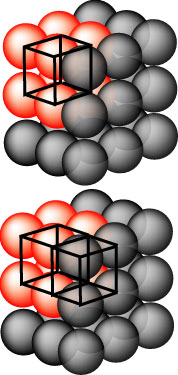The simplest representation of these "space lattices" is in terms of their unit cells. On the right is shown a cubic lattice of atoms and in the upper part the atoms making up the unit cell are in red. The symmetry operations generate identical unit cells in an infinite lattice. A second unit cell is marked in the lower part of the diagram. The points of the unit cell are shown here as occupied by atoms, but it is better to think of the lattice as consisting of a set of points.

 unit cells and repeating unit in a simple cubic solid

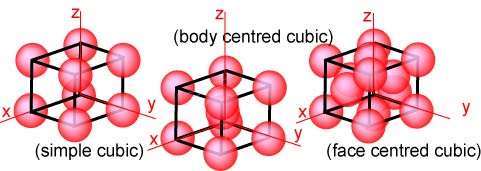
It is only necessary here to consider the cubic lattices, of which there are just the three shown below. They have the obvious names simple, body centred and face centred, but these derive from the more fundamental symmetry conditions mentioned above. There are eleven others, of which one of the most often mentioned is monoclinic, which is the lattice of lowest symmetry. Once again the lattices below are represented in terms of atoms but are really lattices of points.

cubic unit cells, face-centred cubic, body-centred cubic and simple cubic

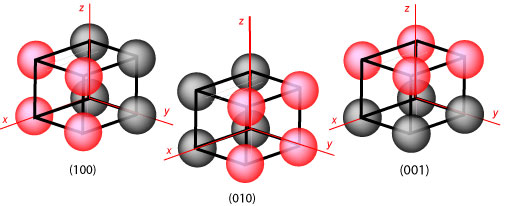
For the determination of structures of solids and for considering the structural characteristics of surfaces the arrangements of lattice points in planes of the crystal are important. The different crystal planes are defined by their Miller indices. The Miller indices of a crystal plane are constructed by determining the intersection of the plane with the x,y,z axes and then taking the reciprocals, by convention written as (hkl). In the examples shown in the diagram below the intercepts of the plane of red atoms are (1,∞,∞), (∞,1,∞) and (∞,∞,1) on going from left to right. Taking the reciprocals of each intercept gives the Miller indices (100), (010) and (001) respectively. Note that each Miller index represents a whole set of planes all parallel to one another. Thus the expression (100) may be used to indicate either an individual plane or the whole set of planes.

the Miller indices of the (100), (010) and (010) planes in a simple cubic unit cell

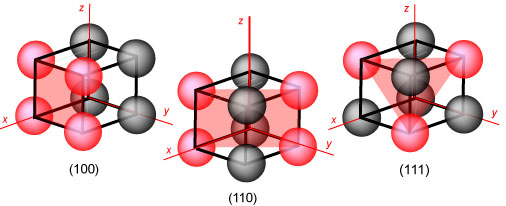
Within the simple cubic cell two other crystal planes are easily identified, the (110) (there will be a set of planes of this type with different orientations, of which the (101) and the (011) are the most obvious, but there are additional ones with negative indices), and the (111). These two and the (100) are the three sets of planes that are most important for basic surface studies. The set is shown below with the atoms on the plane and the plane itself marked in red

the Miller indices of the (100), (110) and (111) planes in a simple cubic unit cell

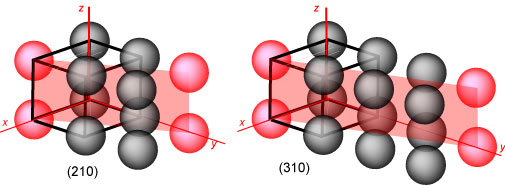
The planes so far shown are low index planes, but there are higher ones. The way to evaluate the indices of these planes requires a slight alteration in the procedure. The intercepts of the plane on the xyz axes are all scaled down by the factor that reduces the highest intercept (other than ∞!) to 1. The diagram below shows the (210) and (310) planes. In the former the intercepts are the set (1,2,∞). These are multiplied by 1/2 and the reciprocals then give (210).

the Miller indices of higher index planes a simple cubic structure

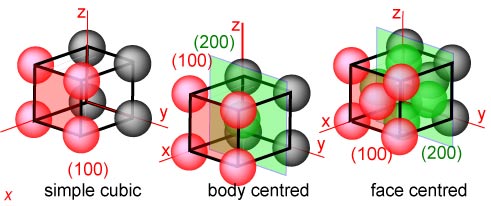
For the three cubic structures the structural arrangement within a plane and between different planes may be different. Below are shown the (100) planes of simple, body centred and face centred cubic lattices. In the body centred and face centred cubic structures there are planes of atoms (marked in green) interleaving the (100) planes. These, together with the (100) planes, make up the (200) set of planes (intercepts (½,∞,∞).

the Miller indices of the (100) and (200) planes in face-centred cubic, body-centred cubic and simple cubic structures

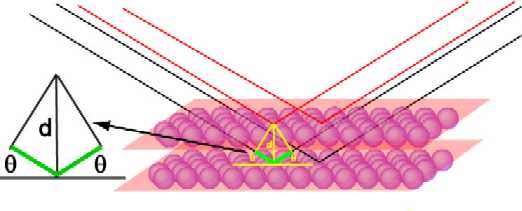
Diffraction from Crystalline Solids

The figure below represents the scattering of radiation from two crystal planes of a solid. The red and black lines represent radiation reflected from the upper and lower set of planes respectively. The reflection is treated as though the two planes of atoms behaved like half-reflecting mirrors. There is a difference of 2dsinθ in the pathlength travelled by the two beams of radiation where d is the perpendicular distance between the planes (the path difference is marked in green and the expanded construction alongside makes the geometry more clear). As the angle of reflection is changed so does the difference in pathlength travelled by the two beams. When the path difference is equal to an integer number of wavelengths the two beams will reinforce one another and when it is an integral number of half wavelengths the two waves will interfere destructively with one another. The intensity of the total reflected radiation will vary sinusoidally with θ. However, if reflection is from a large set of parallel planes the interference builds up so that it is destructive at all angles except those satisfying the constructive interference condition, i.e. when θ is given by

nλ = 2dsinθ

This is Bragg's law. The method of deriving it here is somewhat unsatisfactory but the alternatives would require more effort than you need to put in. However, you may find it useful to visit part of my research website where diffraction in one dimension (from a set of slits) and in two dimensions (an array of holes) is discussed in detail with two illustrative applets.

schematic diagram of Bragg reflection from a crystalline structure

Although the physical model of diffraction given by the Bragg's law approach is not a good one, the law itself is correct. Thus, the (100) planes of a simple cubic structure will give diffraction peaks when

sinθ = nλ/2a, n = 1, 2, 3, ..

where a is the lattice parameter. An alternative way of stating this is to say that there is diffraction from the (100), (200), (300), .. planes at

sinθ = λ/2d, d = a, a/2, a/3, ..

The two statements are equivalent, but the second is much more commonly used. Since Bragg's Law applies to all sets of crystal planes the lattice can be deduced from the diffraction pattern, making use of general expressions for the spacing of the planes in terms of their Miller indices. For cubic structures

d(hkl) = a/(h2 + k2 + l2)1/2

Note that the smaller the spacing the higher the angle of diffraction, i.e. the spacing of peaks in the diffraction pattern is inversely proportional to the spacing of the planes in the lattice. The diffraction pattern will reflect the symmetry properties of the lattice. A simple example is the difference between the series of (n00) reflections for a simple cubic and a body centred cubic lattice. For the simple cubic lattice, all values of n will give Bragg peaks. However, for the body centred cubic lattice the (100) planes are interleaved by an equivalent set at the halfway position. At the angle where Bragg's Law would give the (100) reflection the interleaved planes will give a reflection exactly out of phase with that from the primary planes, which will exactly cancel the signal. There is no signal from (n00) planes with odd values of n. This kind of argument leads to rules for identifying the lattice symmetry from "missing" reflections, which are often quite simple.