Where the question number is enclosed in a button, e.g. 
, you can obtain help or comments about the question by clicking it.
Trinity, 2008
Time allowed: 3 hours.
Answer five questions.
Where the question number is enclosed in a button, e.g. 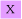, you can obtain help or comments about the question by clicking it.
1.(a) Draw a Jablonskii diagram for a typical aromatic molecule and use it to explain two different routes by which a molecule excited to the S1 state could decay to the ground S0 state without emission of radiation.
(b) Explain the following:
(i) The rate constant for intramolecular intersystem crossing depends on the S1 → T1 energy gap.
(ii) Rates of intersystem crossing are in general only fast if the initial and final states have different electronic configurations.
(c) The aromatic ketone PhCOPh abstracts hydrogen from cyclohexane according to the following kinetic scheme
where C = cyclohexane and P = products. Using the steady state approximation derive an expression for the quantum yield of the hydrogen abstraction reaction.
Discuss what information would be required to determine the rate constant ratios k1/k2 and k3/k4.
(d) The maximum in the absorption spectrum of 1-naphthol is shifted by +3300 cm−1 with respect to the maximum in the absorption spectrum of its conjugate base (both shown below).
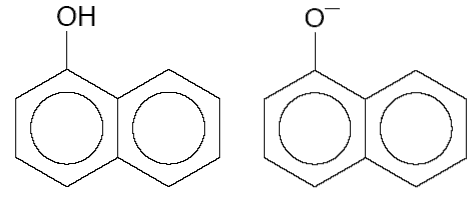
Estimate the difference in pKa values for the S0 and S1 states of 1-naphthol at 300 K.
2.(a) Sketch and explain the typical variation of the surface tension of a surfactant solution over a concentration range from well below the critical micelle concentration to just above it.
(b) The adsorption of a surfactant at the air surface of an aqueous solution obeys the Gibbs equation
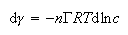
For the ionic surfactant C16TAB (C16H33N(CH3)3+Br−), explain why n = 2 in the absence of salt but n = 1 in the presence of excess NaBr.
(c) The values of surface tension of an aqueous solution of C16TAB, in the absence of salt, at concentrations just below the critical micelle concentration (0.9 mM) at 300 K are given below:
| concentration/10−3M | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| surface tension/10−3N m−1 | 48.0 | 45.3 | 43.1 | 41.2 | 39.5 |
Use the data to calculate the surface excess of the surfactant at the critical micelle concentration and hence calculate the minimum area per molecule at the air/water interface.
(d) Explain qualitatively how the addition of salt will affect the area per molecules at the air/water interface and the critical micelle concentration.
3.Discuss four of the following observations.
(a) The cross section for the reaction H + D2 increases with increasing translational energy Et and can be modelled satisfactorily with the equation%
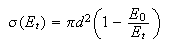
(b) The cross section for the reaction K + HCl(v) → KCl + H increases by a factor of about 100 when HCl is excited from v = 0 to v = 1. Translational excitation of the reactants to the same energy only yields a cross-section enhancement of a factor of 10.
(c) The reaction Ba + HI → BaI (v', j') + H generates highly rotationally excited BaI products with the rotational population distributions peaking at smaller values of j' as v' increases.
(d) The reaction OH(v = 0) + D2 generates HOD products with a vibrational quantum state population inversion in the OD stretching mode, and no excitation in the OH stretch.
(e) The HCl product of the Cl + H2 reaction is backward scattered, the KI product of the K + I2 reaction is forward scattered, and the OH product of the O(1D) + H2 reaction is both forward and backward scattered, relative to the direction of the incident atom.
(f) The photoelectron spectrum of the anion FH2−
shows a series of vibration peaks that may be assigned to a hindered H2
rotational motion in the F-H2− species.
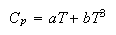
where a = 2 x 10−3 J mol−1 K−2 and b =2.5 x 10−3 J mol−1 K−4.
(i) Explain why the equation has the form given.
(ii) Calculate the entropy of crystalline potassium at 1 K.
(b) A defective crystal of LiF at a temperature T contains ns Li atom vacancies and the same number of F atom vacancies. The changes in entropy and enthalpy of the crystal which take place when the defects are formed are given to a good approximation by the equations
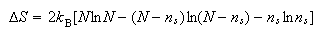
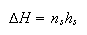
where N equals the total number of available Li sites in the crystal and hs is the enthalpy change when a single Li and F atom vacancy pair forms.
(i) Outline how these equations may be derived.
(ii) Show that at equilibrium and when ns << N, the concentration of defects is given by the equation
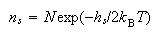
The concentration of defects in LiF is found to double when the temperature is raised from 1000 K to 1100 K. calculate hs.
(c) CO adsorbed on a metal surface at 400 K and measured data for the varition in fractional monolayer coverage of CO, θCO, with CO gas pressure, pCO, are given in the table below.
| pCO/10−4 Pa | 1.0 | 3.0 | 5.0 | 7.0 | 9.0 |
| θCO | 0.16 | 0.36 | 0.49 | 0.57 | 0.63 |
(i) Show that the data conform to the Langmuir isotherm and calculate the absorption constant, b.
(ii) N2 also shows similar adsorption behaviour on the
same surface at 400 K, but with a value of b of 2.4 Pa−1. Suggest an
explanation for the relative values of b for the two gases and calculate θN2 at 400 K when the surface is in contact with a mixture of N2 and CO, with pCO = 5.0 x 10−4 Pa and pN2 = 0.4 Pa.
5.(a) Explain why the spin-spin coupling between two inequivalent protons leads to four separate 1H NMR lines, whereas that between two equivalent protons leads to just one.
(b) Briefly describe the phenomenon of quadrupolar relaxtion in NMR and predict the multiplet patterns that will be seen in typical liquid phase 1H NMR spectra of 12CH3Cl and 11BH4−.35Cl, 37Cl and 11B all have I = 3/2.
(c) The aromatic protons in a tyrosine residue of a small globular protein have the following chemical shifts:
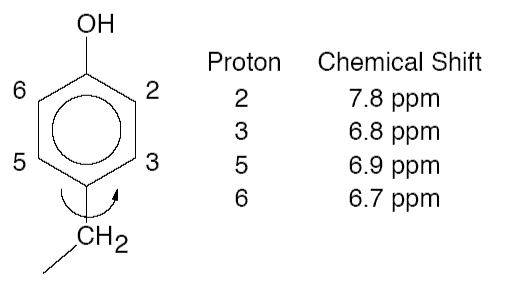
(i) Calculate the differences in 1H resonance frequencies, |ν2 − ν6| and | ν3 − ν5| on a spectrometer with an operating frequency of 500 MHz.
(ii) The rate constant for the indicated 180 degree internal rotation is 2.5 X 10−2 s−1 at 4oC. Assuming an activation energy of 157 kJ mol−1, calculate the rate constants for this "flipping" process at 47oC and 72oC.
(iii) By combining your answers to parts (i) and (ii)
sketch how you would expect the 500 MHz NMR spectrum of the four aromatic
protons to appear at 4, 47 and 72oC.
6. Answer A or B.
A. Discuss the extent to which the following statements are true, giving your reasons.
(a) The wavefunctions exp(+ipx/
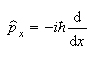
and
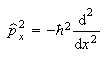
(b) The commutators of x and p, and of x and p2, are
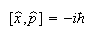
and
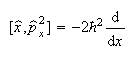
(c) If a large number of identical quantum mechnical systems are each described by the same wavefunction ψ, the measurement of an observable A in each system will give a result equal to the expectation value
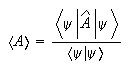
(d) The following normalized wavefunction is a suitable approximation to the 1S state of the helium atom that arises from the 1s12s2 electron configuration:
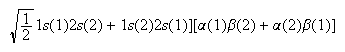
B.(a) How is the canonical partition function Q related to the molecular partition function q for a system of N indistinguishable and non-interacting particles?
(b) Use the relations
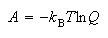
and
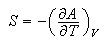
to show that the entropy of such a system is given within the approximation
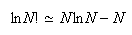
by
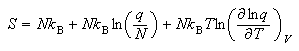
(c) Starting from the expression
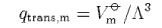
where Vm
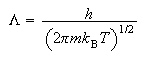
show that the translational contribution to the standard molar entropy of a gas of non-interacting molecules is given by
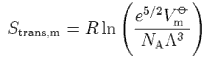
(d) For a gas of diatomic molecules at sufficiently high temperatures the rotational contribution to the standard molar entropy is
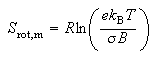
where σ is the symmetry number and B is the rotational constant. Use this result in conjunction with your answer to (c) to account for the differences between the spectroscopic entropies of the following pairs
(i) He: 126, Ne: 146 J mol−1 K−1 (mHe = 4 mu, mNe = 20mu).
(ii) N2: 192, CO: 198 J mol−1 K−1 (mN = 14mu, mC = 12mu, mO = 16mu).
(iii) F2 (T = 250 K): 198, F2 (T = 350 K): 208 J mol−1K−1 (mF = 19mu).
(e) Explain why the standard molar entropy of CO at 298 K
obtained by calorimetry differs from the spectroscopic entropy and is almost
identical to the standard molar entropy of N2.
7. Answer A or B.
A. The diagram below shows one of the fundamental bands in the infrared absorption spectrum of 12C16O2.
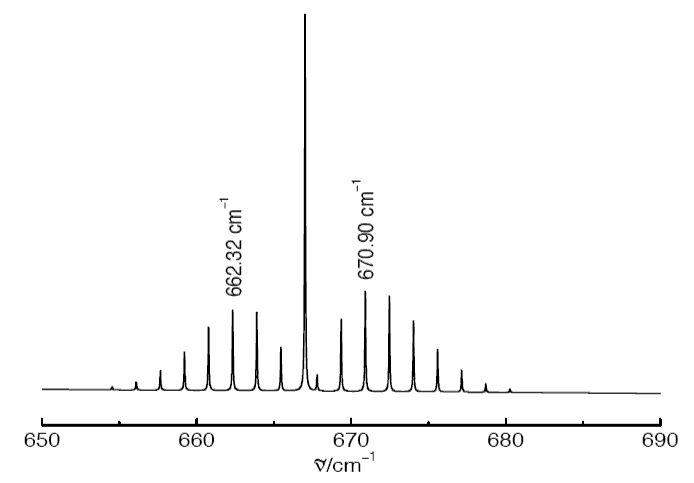
(a) Why does CO2 exhibit an infrared absorption spectrum when O2 does not?
(b) Sketch the normal modes of CO2 and identify the mode that is responsible for the above band.
(c) Explain why only even J levels exist in the ground vibrational state of 12C16O2. Is there a similar restriction on the allowed J levels in the excited vibrational state of the above spectrum?
(d) Assign the transitions that give rise to the two
indicated wavenumbers in the spectrum and use your assignment to estimate
the C=O bond length of CO2. (You may neglect the difference between the
rotational constants in the ground and excited vibrational states.)
B (a) State le Chatelier's principle and illustrate it with a chemical example.
(b) Starting from the expressions
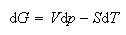
and
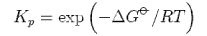
derive the equation
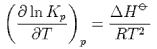
Explain how the equation is consistent with le Chatelier's principle.
(c) How does Kp vary with pressure?
(d) For the following reaction involving perfect gases
show that
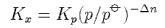
where
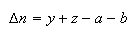
and Kx is the equilibrium constant in terms of mole fraction x. Explain how your answers to (c) and (d) are connected with the principle articulated in (a).
(e) In the gas phase, ethanoic acid partially dissociates
into dimers. At a total pressure of 0.2 bar ethanoic acid is 92% associated
at 298 K and 82% associated at 318 K. Calculate the
enthalpy change for the association reaction.
8. Answer A or B.
A. An ideal solution comprising a mixture of two liquids, 1 and 2, can be defined in terms of the chemical potentials of its components, i
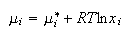
(a) Define the quantities μi, μi* and xi.
(b) If n1 moles of pure liquid 1 are mixed with n2 moles of pure liquid 2 to form an ideal solution show that the Gibb's free energy of mixing is
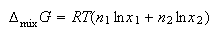
(c) Using your answer to (b), derive expressions for (i) the molar entropy of mixing and (ii) the molar enthalpy of mixing.
(d) For regular solutions the Gibb's free energy of mixing is
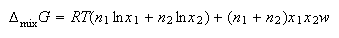
where w parameterizes the non-ideality of the solution. Show that for such solutions the chemical potentials are
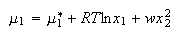
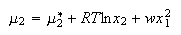
(e) Derive expressions for the activity coefficients of liquids 1 and 2 in the regular solution mixture.
(f) Benzene and CCl4 form regular solutions with w = +324 J mol−1 at 298 K. Would you expect the vapour pressures of benzene and CCl4to be larger or smaller than if the solution were ideal?
(g) Caclulate the enthalpy of mixing for an equimolar
solution of benzene and CCl4 at 298 K and sketch how ΔmixH would vary with the mole fraction of CCl4.
B. The reaction of an aromatic compound (SH) with hydroxide ions in aqueous solution is thought to involve a rapid pre-equilibrium:
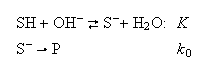
where P denotes the reaction products and
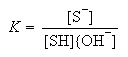
The kinetics of the reaction can be described by the rate law
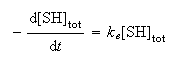
where ke is an effective first order rate constant and [SH]tot is the total substrate concentration.
(a) Show that
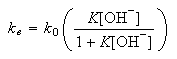
assuming that the pre-equilibrium is maintained throughout the reaction.
(b) Show that the following data are consistent with this kinetic scheme and, using a straight line graphical plot, deduce values of k0 and K
| 102[OH−]/M | 0.2 | 0.4 | 1.0 |
| ke/s−1 | 21.1 | 37.1 | 68.5 |
(d) Suggest an experimental method by which the rate data
in (b) might reasonably have been obtained and explain the physical
principles on which the method is based.