Where the question number is enclosed in a button, e.g. 
, you can obtain help or comments about the question by clicking it.
The problems below are based closely on those set in the Reaction Kinetics course by Mark Brouard.
You should cover the following:
(i) The dynamics of molecular collisions and how they may be studied in molecular beam scattering experiments. The difference between collision and reaction cross-sections. The impact parameter.
(ii) Qualitative understanding of the difference between a centre of mass collision diagram and lab coordinates.
(iii) Conservation of energy and angular momentum in reactions and the role of the impact parameter.
(iv) Qualitative understanding of the role of potential energy surfaces in determining the energy disposal in elementary chemical reactions.
You may find it useful to read Reaction Dynamics by Brouard (OUP Primer).
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
. The reaction
K + HCl (v) → KCl + H
is slightly endothermic for v = 0. The following data were obtained for the reaction cross section σr at different energies, Et:
| Et/kJ mol−1 | 8 | 12 | 20 | 30 |
| 1016σr | 0.33 | 1.08 | 1.7 | 2.0 |
(a) Show that when Et > E0, the threshold energy for reaction, the cross-section data are consistent with the line-of-centres model
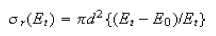
Calculate the threshold energy and the limiting, high collision energy cross-section, πd2,
(b) In terms of the reaction cross-section, the thermal rate constant can be written
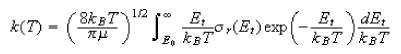
Use this equation to obtain a line-of-centres expression for k(t). Comment on the result you obtain.
You may use the following integral without proof
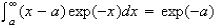
(c) Vibrational excitation of HCl from ν = 0 to ν = 1 increases the reaction cross-section by a factor of about 10. What features of the potential energy surface for the reaction would be likely to give rise to such behaviour?
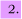. Two reagent molecules A and BC on collision course with
initial velocities
wa and wbc with respect to their centre of mass react to form AB and C. If the final
velocities of the two products are
wab and wc,
show that their final translational energy, Et/, is
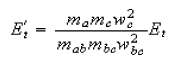
where Et is the initial translational energy.
Discuss the dynamical consequences of the above equation if the atom C acts as a spectator, so that wc = wbc. Under what conditions would you expect spectator dynamics to convert the initial collision energy into product translational energy, product internal energy, or to promote collision induced dissociation?
. The reaction
K + I2 → KI + I
was studied at a centre of mass collision velocity of 800 m s−1 with I2 in thermal equilibrium at 300 K. The reaction cross section was found to be 1.70 nm2.
Using the data below estimate
(a) the total energy available to the products,
(b) the maximum orbital angular momentum, Lmax, of the reactants.
(c) the rotational energy of the KI product if J/ = Lmax where J/ is the rotational angular momentum quantum number for KI.
State any assumptions made in estimate (b).
| : | I2 | KI |
| Dissociation energy/kJ mol−1 | 149 | 319 |
| Vibration frequency/cm−1 | 214.5 | 186.5 |
| Inertial constant/cm−1 | 0.037 | 0.061 |
4. (a) Explain how the constraints imposed by the conservation of angular momentum influence the disposal of rotational energy in a reaction.
(b)Explain why the reaction
Ba + HI → BaI + H
converts orbital angular momentum of the reactants into product rotational angular momentum. A study of this reaction under crossed molecular beam conditions, at a relative reagent velocity, vrel, of 976 m s−1 showed a strong peak in the BaI (v = 0) rotational state distribution at J/ = 420. Given that the orbital angular momentum of the reagents in this reaction can be written L = μvrelb, estimate the most probable impact parameter b of the reactants and the reaction cross section.
[Take the atomic masses to be Ba = 137.3, I = 126.9 and H = 1]
5. The reaction
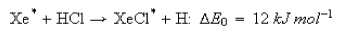
has been studied under molecular beam (Xe*) --- target gas (HCl) conditions. If the mean velocity of the Xe* beam is 2 km s−1 and the target gas molecules are assumed to be stationary, estimate
(i) the energy available for disposal among the reaction products (the target gas is in thermal equilibrium at 300 K),
(ii) the maximum impact parameter for reaction, given Sreact = 2 x 10−14 cm2
(iii) the maximum rotational quantum number J/ of the product
XeCl* in v
(iv) the highest vibrational level v/ that is energetically accessible.
[The atomic mass of Xe is 131; the rotational constant for XeCl* is 0.07 cm−1, and its vibrational frequency is 195 cm−1]
6. (a) When neutral K reacts with Br2 the KBr product is scattered in the forward direction relative to the K atom, with a reaction cross-section that is large compared with the gas kinetic cross-section. Explain how the ionization potential of K (419 kJ mol−1) and the electron affinity of Br2 (245 kJ mol−1) can be incorporated into the harpoon mechanism to account for this. Estimate the reaction cross-section.
[The Coulomb potential between particles of charge q1 and q2 is
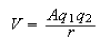
with A = 9 x 109 J C−2 m.]
(b) How would you expect the cross-sections for the reaction to change for Br2 and Cs (ionization potential = 376 kJ mol−1)?
(c) Describe an experiment that could be used to study the angular dependence of the KBr product in the K + Br2 reaction.
7. (a) Briefly outline experimental strategies currently available for measuring the partitioning of energy in between vibration, rotational, and translation in the products of an exothermic atom transfer reaction
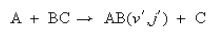
(b) How may the properties for vibrational and translational energy disposal be influenced by the topography of the potential energy surface over which the reaction proceeds, and by the masses of the atoms involved? Illustrate you answer by reference to the data, determined at 300 K, for the following reactions
| reaction | <fvib> | <ftrans> | product scattering |
| H + Cl2 → HCl (v/,j/) + Cl | 0.39 | 0.54 | backward |
| Cl + HI → HCl(v/,j/) + I | 0.71 | 0.16 | forward |
[<fvib> and <ftrans> are the mean fractions of the total energy disposed into vibration and translation]
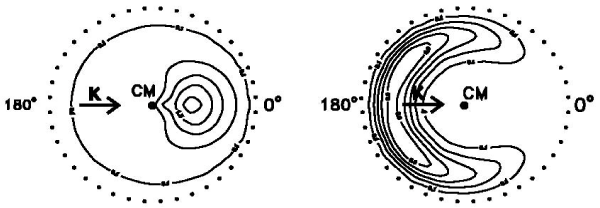
. (a) The figures below show the product KI flux contour plots in the centre-of-mass (CM) frame for the K + I2 (left) and K +
CH3I
(right) reactions (the outer rings of dots show the maximum CM velocities of
KI).
What can be learnt about the dynamics of the two reactions from these figures? You may find the following information helpful. The electron affinities of I2 and CH3I are 222 and −10.6 kJ mol−1 respectively, and the ionization potential of K is 419 kJ mol−1.
The differential cross-section of the reaction
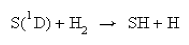
is shown below.
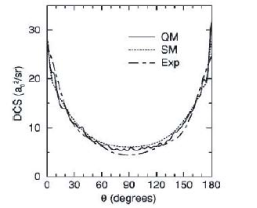
Contrast the scattering behaviour of this reaction with that observed for the two reactions in (a).
9. OH in its ground electronic state undergoes the reaction
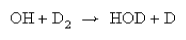
which is isoelectronic with the F + H2 reaction. The figures below show plots of product flux in the centre-of-mass frame for the above reaction (the dashed rings are labelled according to the number of quanta m in the bending mode, and n in the OD stretching mode of HOD(m, n). The experiments were performed under molecular beam conditions, with the D atom products detected by a laser ionization technique.
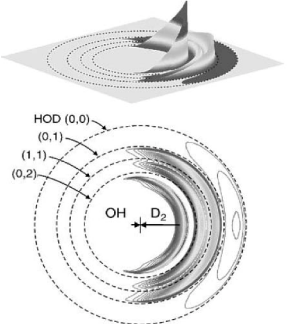
(a) What does the above figure suggest about the mechanism of the reaction?
(b) What spectroscopic experiments might be performed to probe the transition state region of this reaction (or a similar reaction) more directly?