Chemical Potential

First and Second Laws of Thermodynamics

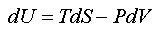
The first and second laws of thermodynamics can be written as
(1) The internal energy U is a state function,
(2) (a) The entropy S is a state function, (b) In an isolated system S is a maximum at equilibrium.

A combined mathematical statement of (1) and (2)(a) is

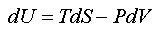
which, for convenience, we rearrange to

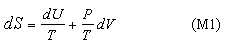
These equations apply to a single component.

Equilibrium in a One Component System: Temperature and Pressure Equilibration

We now apply the second equation (M1) together with the condition (2)(b) to determine the conditions for equilibrium between two sub-systems within a single isolated system and this is done in the panel below.

Although the result, that temperature and pressure are uniform in the system at equilibrium, is not surprising, the method can now be extended to the more interesting situation of a two component system. First, we note that the use of the phrase state function is equivalent to stating that U is a perfect differential, i.e. that

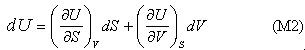
Other arguments, which have not been presented here, make the link between T and P and the two derivatives:

.

Equilibrium in a Two Component System: Temperature, Pressure and Chmeical Potential Equilibration

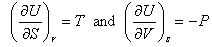Equation (M2) only applies to a single component. For a two component system U will certainly depend on the amounts of each component present and so the complete expression for U should become

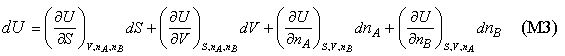
which, for convenience, we abbreviate as

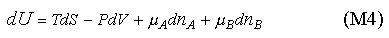
Equation (M4) can be rearranged in the same way as used to obtain (M1). We use the result in the panel below to establish the equilibrium conditions in a two component system, using the same method as for the panel above.

It is more convenient to have a definition of the chemical potential in terms of the Gibbs free energy G. The definition of G is

G = U + PV - TS

from which

dG = dU + PdV + VdP - TdS - SdT

Using equation (M4) we obtain

dG = VdP - SdT + m_Adn_A + m_Bdn_B

By analogy with equations (M3) and (M4) m_A is the same as

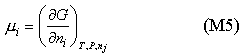
In a two component system the Gibbs free energy contains contributions from the free energies of the two pure substances and from the mixing. The contribution from the pure substance is just G/n where n is the number of moles of substance. The contribution from mixing varies with concentration. This contribution can be obtained in the ideal case by applying equation (M5) to equation (E3) (Entropy of Mixing). The result (derivation) gives a contribution to m_A of RTlnx_A. Because this result combines the two assumptions defining the ideal solution they can be replaced by the single definition of an ideal solution as one for which the chemical potentials of the components are given by