When two pure substances mix under normal conditions there is usually an increase in the entropy of the system. This is qualitatively easily visualised in terms of the increased disorder brought about by mixing. For the mixing of two ideal gases it is straightforward to obtain an expression for the entropy of mixing. Since the molecules of ideal gases do not interact the increase in entropy must simply result from the extra volume available to each gas on mixing. Thus, for gas A the available volume has increased from VA to (VA + VB). By calculating the entropy of expansion of each gas we can calculate the entropy of mixing as shown in the panel below.

The entropy of mixing in equation (E1) can be rewritten
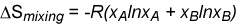
and the Gibbs free energy of mixing is
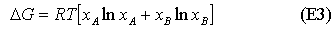
Since the mole fractions in equation (E1) are always less than unity, the ln terms are always negative, and the entropy of mixing is always positive. Its variation with concentration is shown in the diagram below. Similarly, the Gibbs free energy of mixing is always negative and becomes more negative as the temperature is increased (see diagram). The decrease in free energy on mixing is always a strong force promoting mixing.
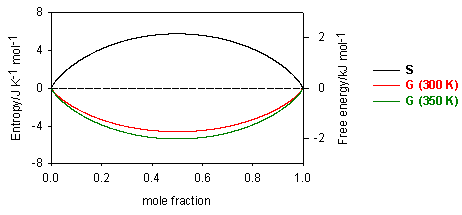
It is interesting to use the entropy and free energy of mixing above to derive the relation between DG and the equilibrium constant K. This is not a standard procedure and is not useful except that it does demonstrate very clearly the role of mixing in helping to determine the position of chemical equilibria.