(i) The Langmuir adsorption isotherm. The underlying assumptions and its derivation using a kinetic model. The Langmuir isotherm has many deficiencies but it is widely used as a model to understand adsorption in gas/solid and solution/solid situations. It is particularly widely used for understanding kinetic processes at interfaces and, for this, you need to understand (and derive) the version of the isotherm for mixtures.
(ii) Surface catalysed reactions (mainly the application of the Langmuir isotherm to surface kinetic models).
(iii) Reaction rates at an electrode. The origin of the Butler-Volmer equation and the Tafel equation. The exchange current density and the reasons why it varies between different electrode materials, particularly for the H2/H+ reaction. The mechanisms of the electrochemical H2/H+ reaction.
(iv) Cyclic voltammetry and its application to simple reactions.
The material on adsorption is covered in Atkins: Physical Chemistry. For the electrochemical interface you may find the Oxford Primer, Electrode Dynamics by Fisher, useful. The relevant lecture course is that on Interfacial Kinetics by Richard Compton.
For comments and help click the button numbering the question.
The following results were obtained for the volume (corrected for STP) of nitrogen adsorbed on to a high surface area carbon sample at 283 K:
| 283 K | - | - | - | - |
| P/Torr | 100 | 300 | 500 | 700 |
| V/cm3 | 9.0 | 23.1 | 34.3 | 43.4 |
Find the volume of nitrogen corresponding to complete coverage of the surface. Assuming that each nitrogen molecule occupies an area of 0.16 nm2, estimate the surface area of the carbon sample.?
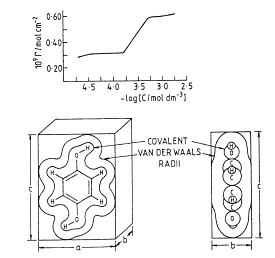
Hydroquinone adsorbs as a monolayer from aqueous solution on to smooth polycrystalline platinum electrodes. The packing density (Γ/mol cm-2) versus adsorbate concentration (C/mol dm-3) is shown in the diagram below along with the structure and size of the hydroquinone molecule.
The adsorption of a species A on a surface from a mixture of A and B is given by the equation
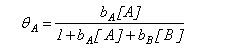
Explain why the concentration of B appears in the denominator of the right hand side of the equation.
By assuming that the rate of a heterogeneous reaction is proportional to the coverage(s) of the appropriate species, use the equation above to calculate the rates of reaction on the surface (i) when initially adsorbed molecules of type A are converted to type B in a unimolecular reaction and (ii) when a bimolecular reaction of A and B occurs. Hence comment on the following observations:
(a) The rate of decomposition of N2O on a surface
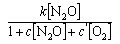
(b) The rate of decomposition of NH3 on Pt
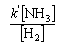
(c) The rate of hydrogenation of ethene on Cu
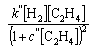
where c, c', c'', k, k', and k'' are constants.
Consider the following mechanism for the surface catalysed unimolecular reaction of species A:
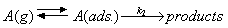
Derive an expression for the rate of formation of the products in terms of k2 and the adsorption constant K in the Langmuir isotherm (see your results for question 3). How would you expect the rate to depend on the temperature?
Methanoic acid decomposes on the surface of gold to give H2 and CO2. At 340 K the initial rate varies with the initial pressure of methanoic acid as follows:
| 105 x rate/Torr min-1 | 0.45 | 0.76 | 1.00 | 1.45 | 1.75 | 2.13 |
| pressure/Torr | 2.5 | 5.0 | 7.5 | 15 | 25 | 50 |
Use the Langmuir isotherm to interpret these data and to obtain a value of the rate constant for the surface reaction.
What is the order of the reaction at (a) the high pressure limit and (b) the low pressure limit?. Comment on these changes.
5. If an electrode is connected as an anode in an electrolytic cell, over a certain range of the overpotential η the current flowing, i, can be shown to be related to η by an equation of the form
i = i0exp{(1 - α) Fη/RT
where F is the Faraday constant. What interpretation is to be placed on the constant α in this equation? The following measurements were made at T = 298 K of current i as a function of η in a cell where the electrode was made positive
| i/10-5 A | 15.9 | 25.4 | 164.3 | 1063.4 |
| η/10-3 V | 75 | 100 | 200 | 300 |
How far are these data consistent with the simple expression, and what value of α do they predict?
Do you expect this equation to work at values of η of around 10 mV?
At applied voltages significantly far from the equilibrium electrode potential the current at a cathode varies with overvoltage η (η = E-E 0 according to the equation
logi = logi0 - ηα F/2.3RT
where α is often about 1/2. Explain briefly the origin of this equation.
The concentrations in the cathode compartment of a cell containing NaOH solution are such that at the mercury cathode the equilibrium potentials, E0 for sodium and hydrogen are respectively -1.87 and -0.83 V. For H2 and Na i 0 is 10-12 and 10-2 A cm-2 respectively. In each case α is close to 1/2. Calculate the ratio of sodium to hydrogen liberated at the cathode when it is operated at -2.0 V. Note that the sodium dissolves in Hg to form an amalgam which is kinetically stable under the conditions of hydrolysis.
(a) For the electrode reaction
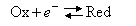
the net current, i, depends on the applied potential,η = E − EO, as
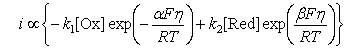
Explain the meaning of the various terms in the equation.
(b) It has been proposed that Step 1 in the hydrogen evolution reaction at a metal electrode is
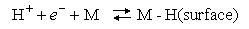
The second step in the proposed mechanism may be either A or B below:
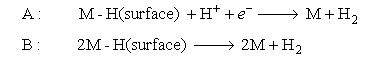
(i) Write an expression for the current in the situation when Step 1 is rate determining.
(ii) When either A or B are rate determining Step 1 may be treated as an equilibrium. In this case, by assuming that the forward and backward rates of Step 1 are equal, and that the transfer coefficients are 1/2, show that the isotherm for the initial adsorption (i.e. Step 1) is
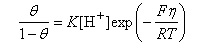
where K is a constant and θ is the coverage.
(iii) Close to the equilibrium potential the term on the right hand side of the above equation is small in comparison with unity and hence (1 - θ) ≈ 1. Use this to write expressions for the overall rate of the reaction when A or B are rate determining and hence show that the currents in the two cases are respectively (taking the transfer coefficient in A to be 1/2)
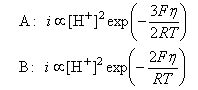
(iv) The following i - η data for the evolution of hydrogen on a metal at 300 K have been obtained:
| i/A cm−2 | −10−4 | −5x10−4 | −2.5x10−3 | −10−2 |
| η/V | −0.010 | −0.031 | −0.052 | −0.070 |
Which of the three possible mechanisms above account best for this behaviour? Take RT/F to be 0.0258 V.
(c) The exchange current densities for the hydrogen evolution reaction in 1 mol dm−3 acid and the strengths, EM H, of the corresponding M-H bonds are given for a number of metals in the table below. To what extent are these data qualitatively consistent with the mechanism in part (b)?
| metal | Zn | Ni | Pt | W | Ti |
| i0/A cm−2 | 10−10 | 3x10−8 | 10−5 | 10−9 | 10−11 |
| EM H/kJ mol−1 | 8 | 12 | 15 | 18 | 20 |
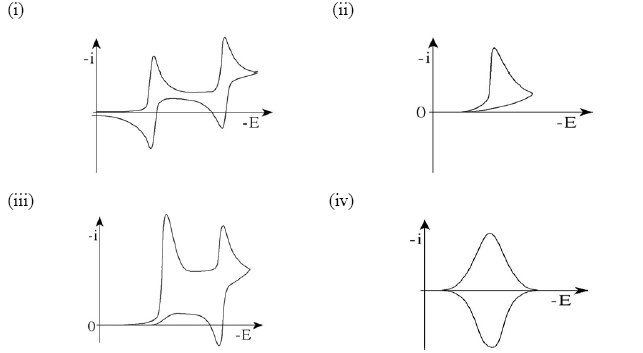
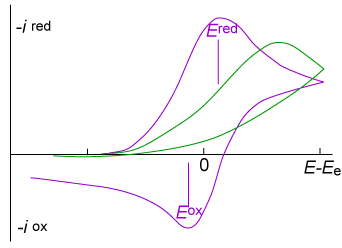
8.(a) The figure below show typical cyclic voltammograms for reversible (purple) and irreversible (green) single-electron reductions at an electrode surface. Discuss the shapes of the two plots.
(b) Typical cyclic voltammograms are shown below for
(i) two sequential reversible 1 e electron transfer reactions,
(ii) an EC reaction with a fast chemical step,
(iii) an ECE reaction,
(iv) a surface bound electroactive species.
Describe the features of the voltammograms that are characteristic of each process.