Where the question number is enclosed in a button, e.g. 
, you can obtain help or comments about the question by clicking it.
Apart from the new lecture material on lasers you should go carefully through the spectroscopy problems in the second year. The laser questions involve a lot of this spectroscopy.
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
A pulsed electrical discharge in a mixture of CO2, N2 and He at atomspheric pressure is used to create a population inversion and hence lasing action on the (0,0,1) → (1,0,0) band of CO2. The (0,1,0), (1,0,0) and ((0,0,1) energy levels of CO2 are at 667, 1388 and 2349 cm−1, and N2 (v=1) is at 2331 cm−1.
(a) Explain the collisional processes between N2 and CO2 which lead to the population inversion.
(b) The (0,0,1) level has 1Σu symmetry. Explain the meaning of this symbol and draw an energy level diagram for the rotational states J' in this upper vibrational level for the 12C16O2 isotopomer.
(c) The rotational states in the 1Σu+ (0,0,1) level can be regarded as having a temperature of 400 K and the most populated rotational level is J'= 19. Estimate the value of the rotational constant B in this state.
(d) Spontaneous emission in the (0,0,1) → (1,0,0) band, which originates from J'= 19, occurs as two lines at 944.194 and 974.622 cm−1. Assign these lines and deduce the value of the rotational constant B in the (1,0,0) level.
(e) Laser gain g(ν) is given by the equation
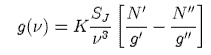
where K is a constant, SJ = J'+ 1 for a P branch transition and SJ = J' for an R branch transition, ν is the transition frequency and N' and N" are populations in the upper and lower levels respectively with degeneracies g' and g". Show that if N" is zero the gain will be larger for the lower of the two wavenumbers at which emission occurs for a given J' in the (0,0,1) → (1,0,0) transition. How might the laser cavity be constructed to ensure that lasing occurs on the higher wavenumber?
(f) The (1,0,0) lower lasing level does not radiate to the ground state. Explain why this is and give an account of the processes leading to population losses in the (1,0,0) level.
(g) The lowest frequency vibration-rotation absorption band of CO2 has P, Q and R branches. The first three P branch lines are at the following wavenumbers: 665.820, 664.263 and 662.710. Explain why there is P, Q and R branch structure, assign quantum numbers to the three P branch lines, and calculate the rotational constants in ground and excited states (you may neglect centrifugal distortion). Comment on the relative values of B for these states and for the value in the (1,0,0) state calculated above.
(h) From your value of B for the ground state calculate the CO bondlength in CO2.
2. The He Cd laser operates at 441.6 nm on an electronic transition in the Cd+ ion and can be considered as a three level system as shown below.
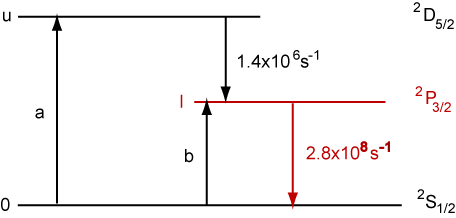
The ground level 0 has the term symbol 2S1/2 and is pumped continuously at a rate a (ions per unit volume per second) to the upper level u (2D5/2) and at a rate b to the lower laser level l (2P3/2). Radiative rates are as shown. (The levels are excited by a combination of collisional processes involving He metastables and electron impact excitation.)
(a) Give the degeneracies of the states u and l.
(b) Write down steady state expressions for Nu and Nl making the assumption that pumping rates a and b and the radiative rates on the diagram are the only kinetic processes.
(c) Show that gain would be possible when b < 132.3a.
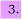A three level system is shown below where ku and kl are the radiative rate losses from u and l respectively (assume that they are the only loss processes), and assume that the pumping pulse populates u in a time which is short compared with 1/ku.
(a) Write an equation to show the time dependence of Nu.
(b) Show that the lower lasing level will have a time dependent concentration Nl of the form
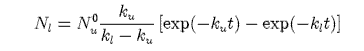
where Nu0 is the concentration in the upper level at time zero.
(c) Taking the u and l levels to have the same degeneracy, deduce the condition for positive gain on the system as a function of time.
(d) Show that if kl > 2ku gain will always be positive. Calculate the time for which gain will be positive in the case when kl = 0.5ku = 2×106 s−1.
4. The Cu vapour laser operates as a three level system as shown below. The u level is excited by electron impact excitation of Cu vapour.
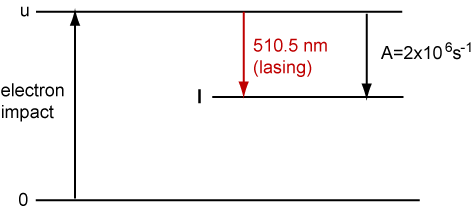
Cu vapour at a concentration of 1023 atoms m−3 is subjected to a pulsed discharge which produces electrons whose kinetic energy can be described as a Maxwell-Boltzmann distribution at a temperature of 15000 K and a density of 1019m−3. The velocity averaged cross section of Cu from the ground states to the upper level is 10−22m2.
(a) Calculate the mean velocity of the electrons from the kinetic theory of gases.
(b) Use the relationship for a bimolecular rate constant (k = cross section × velocity) to calculate the value of k for electron impact excitation of the upper level. Hence calculate the rate of excitation of the upper level.
(c) The typical gain g(ν) of a Cu vapour laser at the line centre is approximately 5 m−1 and is given by g(ν) = 8.6×10−18Num−1, where Nu is the upper state concentration in atom m−3. From your value of the rate of excitation calculate the time for the upper state population to reach a point where there is a gain of 5 m−1. Assume that the rate of excitation is constant and ignore losses resulting from stimulated emission.
(d) The A factor for spontaneous radiation from the upper to the lower lasing level is 2×106s−1. Is it reasonable to neglect this?
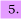The oxygen-iodine chemical laser operates by the reaction
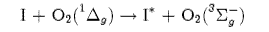
(a) Deduce the term symbols for I and I* and comment on the relative concentrations of these spin-orbit states required to produce a population inversion. Is the optical transition between I and I* allowed?
(b) Discuss the orbitals which give rise to the ground X and first excited a state of O2. Is the optical transition between the X and a states allowed?
(c) The spin orbit splitting in ground state I atoms is 7603 cm−. The O2 a (1Δg, v = 0) level lies 7882 cm− above the ground state of O2. Explain why the equilibrium constant K for the laser reaction above is only weakly temperature dependent. Is the reaction spin allowed?
The reaction
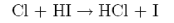
produces HCl in vibrationally excited levels with relative populations
| ν | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.4 | 1.0 | 0.8 |
(a) Explain why this reaction produces a population inversion and a large fraction of the available energy in vibration (70%) despite having a late barrier.
(b) A short time after the initiation of reaction the vibrational energy remains inverted while the rotation energy levels can be represented by a Boltzmann distribution close to room temperature. Explain why.
(c) When the rotational levels are in equilibrium but the vibrational levels are populated as above, the highest gain is found on a transition originating from J = 4 in vibrational level ν. Identify the transition and calculate its wavenumber. [For HCl ωe = 2991 cm−1, xeωe = 53 cm−1, B = 10.6 cm−1. Assume B is independent of ν and ignore centrifugal distortion.]
7. A necessary condition for gain on a transition between two quantum states is that the factor F must be positive, where
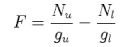
Nu and Nl are the populations and gu and gl are the degeneracies of the upper and lower states respectively.
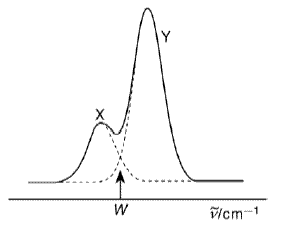
(a) Two absorption bands X and Y as shown above ocur in the spectrum of a gaseous alkyl iodide RI. Absorption in each of the bands results in photodissociation with a quantum yield of unity, to different products
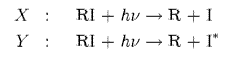
where I and I* are the lower and upper states that arise from the lowest energy electron configuration of the iodine atom. The absorption cross section s is each band can be described by a Gaussian function,
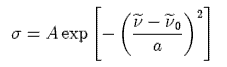
where ν is the wavenumber and ν0 is the band centre. The values of A, ν0 and a are given below:
| Band | A/10−21m2 | ν0/cm |
a/cm−1 |
| X | 1.0 | 37000 | 4800 |
| Y | 3.0 | 48000 | 4800 |
The total absorption cross section is the sum of the two Gaussians.
(i) What are the term symbols and degeneracies of the two states of iodine, I and I*.
(ii) Calculate the lowest wavenumber at which photodissociation can produce a positive value of F for the I*-I transition.
(iii) Explain why this wavenumber is not the same as the wavenumber, W, shown in the diagram, at which the absorption cross sections of the two bands are equal.
(iv) For the process producing a ground state I atom
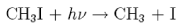
the I atom is found to have a centre of mass velocity of 560 m s−1 for photolysis at 266 nm. Calculate the centre of mass velocity of the CH3 fragment. Hence obtain the amount of energy partitioned into internal energy of CH3, given that the dissociation energy D00 of CH3I is 230 kJ mol−1.
(v) The quantum yield for dissociation of CH3I in the gas phase is equal to unity, but different values are obtained in solution. In solution the quantum yield depends both on photolysis wavelength and on the nature of the solvent. Account for these observations.
(b) (i) A diatomic closed shell molecule is formed with its first two vibrational levels having populations in the ratio N1/N0 = x. The rotational levels in both vibrational states are in thermal equilibrium at temperature T. Show, using the equation at the beginning of the question, that the gain is positive on a P branch transition when
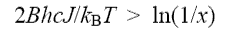
where J is the rotational quantum number of the lower level. The rotational constant B can be assumed to be the same for the two vibrational states.
(ii) The gain will be close to its maximum value when the upper lasing level has its quantum number equal to Jmax, the most populated level in ν = 1. Obtain the value for Jmax for a molecule with B = 1.9 cm−1 at a rotational temperature T = 300 K. Hence show that this leads to gain on the P-branch transition when x < 0.86, i.e. a laser on this transition can operate on a partial vibrational inversion. Find the appropriate value for x to be positive for gain to be positive on the R-branch transition originating from upper level Jmax.