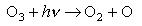
It is important to familiarize yourself with some of the apparently strange ideas of quantum theory because these will later play a crucial role in our understanding of valence, etc. At this stage it would be most useful to read a semi-popular description of the development of quantum theory (there are many books at this level of which Mr Tompkins in Paperback by George Gamow, The Strange Story of the Quantum by Banesh Hoffman, and The Quantum World by J.C.Polkinghorne are three).
Crystallize your understanding by writing a summary of the evidence for (i) quantization, and (ii) particles behaving as waves. To what extent are the two phenomena connected? You might find it useful to have some advice on how to answer "essay" type questions.
Then do the problems below, which also focus on the interaction of electromagnetic radiation with molecules and atoms.
Click here for values of fundamental constants
1. 1. In classical mechanics the linear momentum p of a moving particle is p =mv where m is its mass and v is its velocity. Since v may take any value, the momentum may have any value. A quantum mechanical particle has a wavelength given by de Broglie's relation,
λ = h/p
where h is Planck's constant. When the particle is confined to a box the wavelength can only take on values corresponding to standing waves in the box. Thus, for a one dimensional box the momentum of the particle may only have the values
p = nh/a
where n is an integer (quantum number) and a is the dimension of the box.
Use de Broglie's relation to write down an expression for the kinetic energy of the quantum particle and use the result to calculate how much energy is required to increase the momentum by one quantum for (i) an electron (ii) a hydrogen atom, (iii) a benzene molecule, (iv) a cricket ball (weight 5.75 ounces), each in a box of length 10 times the dimension of the object. Give your values in eV or cm-1 (it is not customary in quantum mechanics to use J mol-1 as units). Comment on your results.
2. In classical mechanics the angular momentum p of a rotating object is given by
p = Iω
where I is its moment of inertia and ω is its angular velocity. What are the units of angular velocity? As for linear momentum, ω may take any value and so the angular momentum may have any value. For a quantum mechanical particle the angular momentum is quantized in quanta of h/2π and the angular momentum of the particle only has the values
p = [l(l+1)]1/2h/2π
where l is an integer (sometimes, as for the spin of an electron, l may take half integer values). Use this expression for the momentum to calculate the rotational kinetic energy in the l = 1 state of (i) the nucleus of a hydrogen atom (take I = 3ma2/5 where a is the radius of the nucleus and m is its mass), (ii) a hydrogen atom (take I = μr2, where r is the mean distance from the nucleus to the electron (guess a value) and μ is the reduced mass), (iii) a hydrogen molecule (same formula as (ii) and look up the interatomic distance, (iv) a cricket ball (same formula as (i)). As before, give your values in eV or cm-1. Comment on your results.
3. The molecules in a gas have thermal energy in the form of energy of translation, rotation and vibration and it is this energy that determines their temperature. The average rotational energy is found to be 3/2RT per mole. Taking the mean rotational energy of each of the objects in question 2 also to be 3/2RT per mole, use your results from question (2) to estimate the mean value of each of their angular momentum quantum numbers. Comment on your results.
4. Sketch a diagram of the electromagnetic spectrum showing the relative frequencies and wavelengths of microwave radiation, visible light, x-rays, infrared radiation, ultraviolet radiation, long wave and medium wave radio, and γ-rays. To give you a start the visible spectrum and its wavelengths are shown below. The diagram shown is an applet, which means that it is calculated on the spot rather than stored (Click here for information concerning applets; the relevant filenames, if you wish to download them, are respectively tutorials/quantum/atomic/atomic.jar and tutorials/quantum/atomic/AtSpectraAppletJ.html).
Using the following information identify what type of molecular and atomic processes occur in the different regions of the spectrum.
(i) The ionization energy of the hydrogen atom in its ground state is 13.60 eV.
(ii) A dye has a strong absorption band at a wavenumber of 17000 cm-1.
(iii) In the upper atmosphere ozone undergoes the following photochemical reaction
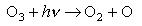
The energy required to dissociate a mole of ozone by this route is about 400 kJ mol-1.
(iv) A diatomic molecule behaves as a harmonic oscillator with a frequency ν given by
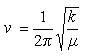
where k is the force constant and μ is the reduced mass (= m1m2/(m1 + m2)). The force constant for HCl is 530 N m-1.
(v) X-ray diffraction from crystals is usually done with wavelengths of about 1 Å.
(vi) The bond length of CO is 0.1128 nm. Calculate its moment of inertia (see question 2) and hence the energy of electromagnetic radiation required to excite between states where the rotational quantum number changes from 0 to 1.
(vii) The difference in energy between the two orientations of a proton nucleus in water in a magnetic field is about 2.5 x 10-26 J molecule-1. Excitation between such states is the basis of nuclear magnetic resonance (NMR).
(viii) The commentary on the cricket test matches is on Radio 4 medium wave at 195 kHz.
Include microwaves and γ-rays in the diagram. Find out the typical frequency used in a microwave oven and the response of the molecules in the system being heated. What are the effects of γ-rays on molecular species?