Where the question number is enclosed in a button, e.g.  , you can obtain help or comments about the question by clicking it.
, you can obtain help or comments about the question by clicking it.
You need to know some quantum mechanics at the level defined by the problems below.
There are many excellent books on quantum mechanics but the most suitable is Atkins: Quantum Mechanics, Chapters 1-3. You should try to understand these three chapters or their equivalent but, even if you cannot totally understand the concepts and some of the mathematics clearly, make sure that you can do the necessary manipulations.
Where the question number is enclosed in a button, e.g.  , you can obtain help or comments about the question by clicking it.
, you can obtain help or comments about the question by clicking it.
1. (a) State the Schrödinger equation for a
one-dimensional quantum particle of mass
 .
.
(b) What is Born's interpretation of the wavefunction
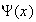 ,
and what conditions must
,
and what conditions must
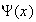 satisfy to be physically acceptable?
satisfy to be physically acceptable?
(c) A particle is subject to the potential
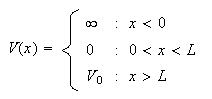 with
with
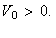
(i) Sketch the potential.
(ii) Show that the wavefunction
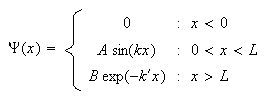 satisfies
the Schrödinger equation with energy
satisfies
the Schrödinger equation with energy
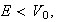 provided
provided
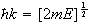 and
and
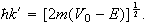 The constants
The constants
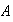 and
and
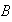 need not be determined.
need not be determined.
(iii) Explain why
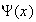 is not physically acceptable unless
is not physically acceptable unless
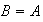 exp(
exp(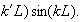
(iv) Provide an argument to show that for
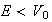 the region
the region
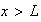 is classically forbidden.
is classically forbidden.
(v) Show that the probability
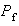 that the particle is found in the classically forbidden region is
that the particle is found in the classically forbidden region is
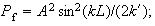 and that the expectation value of the kinetic energy is
and that the expectation value of the kinetic energy is
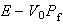 .
You may assume that
.
You may assume that
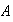 has been chosen so that
has been chosen so that
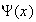 is normalized.
is normalized.
2. (a) Show by direct substitution that the function,
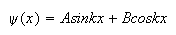 where
where
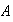 ,
,
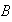 and
and
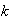 are constants, is a solution of the Schrodinger equation
are constants, is a solution of the Schrodinger equation
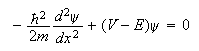 for a particle of mass
for a particle of mass
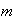 in one dimensional free space for which the potential,
in one dimensional free space for which the potential,
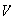 ,
is zero everywhere.
,
is zero everywhere.
Obtain the energy,
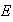 ,
in terms of
,
in terms of
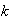 and
and
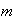 .
.
(b) Consider a particle in a one dimensional box of length
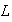 ,
where
,
where
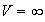 for
for
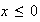 and
and
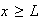 and
and
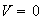 for
for
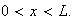
(i) What value must the wave-function adopt at
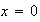 and
and
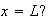
(ii) Show that the condition can be satisfied at
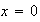 by the function
by the function
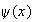 in part (a).
in part (a).
(c) Sketch the probability distributions for a particle in the four lowest energy levels in the box described in part (b). How do these compare with the probability distribution of a classical particle in a box?
(d) For a particle of mass
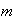 moving in a square two dimensional box of side
moving in a square two dimensional box of side
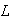 ,
the energy levels are given by the expression
,
the energy levels are given by the expression
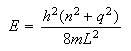 where
where
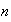 and
and
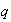 are two independent quantum numbers taking on the values 1, 2, 3,... By
referring to this example, explain the meaning of
degeneracy, as used in quantum mechanics, and deduce
which of the six lowest energy levels in this problem exhibit
degeneracy.
are two independent quantum numbers taking on the values 1, 2, 3,... By
referring to this example, explain the meaning of
degeneracy, as used in quantum mechanics, and deduce
which of the six lowest energy levels in this problem exhibit
degeneracy.
 (a) Sketch (i) the radial wavefunctions and (ii) the
radial distribution functions for an electron in the 1s, 2s and 2p orbitals of
the hydrogen atom.
(a) Sketch (i) the radial wavefunctions and (ii) the
radial distribution functions for an electron in the 1s, 2s and 2p orbitals of
the hydrogen atom.
(b) The normalised wave-function for an electron in the 1s orbital of the H atom is
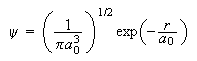 where
where
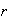 is the electron-nucleus separation and
is the electron-nucleus separation and
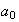 is a constant.
is a constant.
(i) Write down an expression for the radial distribution function describing
the probability of finding an electron between
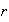 and
and
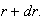
(ii) Using your answer to part (i), calculate the most probable
electron-nucleus separation in terms of
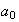 .
.
(iii) By calculating the expectation value
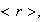 determine the mean distance of the electron from the nucleus in terms of
determine the mean distance of the electron from the nucleus in terms of
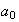 .
.
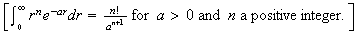
4. (a) What is meant by the Born interpretation of a quantum mechanical wave-function? Describe how the Born interpretation leads to the imposition of boundary conditions for the wave-function of a particle confined to motion on a ring.
(b) The potential energy,
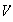 ,
for a harmonic oscillator is given by
,
for a harmonic oscillator is given by
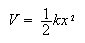 where
where
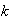 is the force constant and
is the force constant and
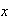 is the displacement from equilibrium. Show by direct substitution that the
wave-function
is the displacement from equilibrium. Show by direct substitution that the
wave-function
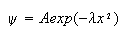 where
where
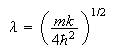 is a solution of the Schrodinger equation for a harmonic oscillator of mass
is a solution of the Schrodinger equation for a harmonic oscillator of mass
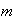 .
Determine the corresponding energy, expressing your answer in terms of the
vibrational frequency,
.
Determine the corresponding energy, expressing your answer in terms of the
vibrational frequency,
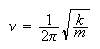
(c) Determine the position of maximum probability density for this wave-function. How does the result compare (qualitatively) with the time averaged probability of finding a particle at a specific location in a classical harmonic oscillator?
(d) Assuming the harmonic oscillator is a reasonable description of the vibration of a diatomic molecule, explain briefly why
(i)
D has a lower zero point energy than
H
has a lower zero point energy than
H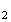 .
.
(ii)
N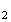 has a higher vibrational frequency than
O
has a higher vibrational frequency than
O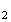 .
.

 The normalized wave-function for an electron confined to a
1-dimensional box, with infinitely high walls, is
The normalized wave-function for an electron confined to a
1-dimensional box, with infinitely high walls, is
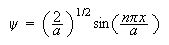 in which
in which
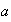 is the length of the box,
is the length of the box,
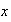 the position along the box, and
the position along the box, and
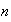 an integer. The Schrodinger wave equation in one dimension is
an integer. The Schrodinger wave equation in one dimension is
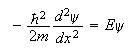
(a) Sketch the appearance of
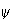 for
for
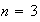 and for
and for
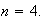
(b) A simple model of the
 electrons in a conjugated molecule treats them as being confined to a
1-dimensional box.
electrons in a conjugated molecule treats them as being confined to a
1-dimensional box.
(i) Estimate a value for the length of the box from the geometry of butadiene.
(ii) Use the Pauli exclusion principle to give the occupancy of the orbitals.
(iii) Calculate the lowest energy transition that can take place among electrons confined to the conjugated system of butadiene.
(iv) The walls of the box in butadiene are not infinitely high. How would a typical wave-function be modified if walls of infinite height were replaced by walls of finite height?
(v) Calculate the probability of finding an electron in the
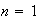 orbital within 0.1 nm of the left hand wall of the box with infinitely high
walls.
orbital within 0.1 nm of the left hand wall of the box with infinitely high
walls.