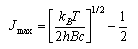
This is an introduction to various aspects of quantized rotation and most particularly to methods of studying rotational energy levels, i.e. rotational spectroscopy using the Raman effect, microwave spectroscopy, far infrared spectroscopy and infrared vibration-rotation spectroscopy. The problems cover aspects of each of these. Before doing the problems you should study the following topics below. Once you have done this you will find it helpful to use the infrared spectroscopy and the Raman spectroscopy applets (interactive calculations) to look in more detail at vibration-rotation spectra (topic (v)) and pure rotation spectra (topic (iii)) respectfully.
The basic topics to cover are:
(i) The rotational energy levels of molecules in the gas phase. The quantitative treatment of the rigid rotor model for linear molecules. A qualitative discussion of the extra complications in the rotational energy levels of symmetric top molecules. A qualitative understanding of the effects of centrifugal distortion on the energy levels.
(ii) The population of rotational levels as determined by the competition between Boltzmann factor and degeneracy of the level. Special effects arising from Bose-Einstein or Fermi-Dirac statistics both in spectroscopy and in heat capacities (you may find it useful to refer ahead to the rotational heat capacity applet in statistical mechanics.). Consider especially the examples H2, D2, CO 2, and C2H2 .
(iii) Selection rules for pure rotational spectra in microwave, infrared, and Raman spectroscopy. The intensities of the lines and the overall appearance of the pure rotational spectrum in the infrared and Raman. Determination of the rotational constants from the spectrum.
(iv) The quantitative use of rotational spectra to determine bondlengths. Consider what type of molecules can be studied in this way. The use of isotopic substitution to gain extra information.
(v) The rotational fine structure in a vibration rotation band. P, Q and R branches and the general appearance of the band. Combination sum and difference plots for determining the rotational constants.
Infrared rotational spectra are excited by electromagnetic radiation in the far-infrared region of the spectrum, 10 - 200 cm−1 and are always observed in absorption. Thus, only increases in the rotational quantum number are observed. Normally, for a molecule to absorb in the far infrared it must have a permanent dipole moment (this is alos true for the closely related microwave spectrum). Molecules with permanent dipole moments do not show any spin statistics in their rotational spectrum because they do not have any symmetry at right angles to the main axis of symmetry of the molecule (if there is one). Suggested "experiments" are
(i) The B slider controls the value of B. You will be able to observe that the spacing of the lines is approximately 2B. You should write out the formula for the lines to see why this is.
(ii) With the value of B fixed vary the temperature and note how the maximum moves further from the band origin as the temperature increases. The reason for the maximum is that as J increases the increasing degeneracy (2J + 1) favours a higher population but the decreasing Boltzmann factor favours a lower one. The different rate at which these factors change generates the maximum. The actual population of the levels and the number of transitions occurring between levels is shown on the right hand side of the diagram.
(iii) Note the effect of varying the distortion constant D. This covers a realistic range in this diagram but only has a relatively small effect, and then only on the highest frequency lines. Why are only the highest frequency lines affected?
A Raman spectrum is excited by electromagnetic radiation in the visible region of the spectrum, 15000- 20000 cm−1, 700 - 400 nm, a long way from energies associated with rotational transitions (far infrared). To emphasize this difference the spectrum is shown as it might actually appear in the upper half of the diagram and is plotted as a function of wavelength. The unchanged Rayleigh line always appears very strongly (more strongly than shown) at the centre of the spectrum. Since this is a pure rotation spectrum only the ground state value of B affects the spectrum. A slider to vary the centrifugal distortion constant is included with values in the range typical of these types of molecules, but the effect, which is just visible, only really shows up in quantitative calculations. Suggested "experiments" are
(i) The B (lower) slider controls the value of B. You will be able to observe that the spacing of the lines is approximately 4B. You should write out the formula for the lines to see why this is.
(ii) With the value of B fixed vary the temperature and note how the maxima in the O and S branches move further from the band origin as the temperature increases. The reason for the maximum is that as J increases the increasing degeneracy (2J + 1) favours a higher population but the decreasing Boltzmann factor favours a lower one. The different rate at which these factors change generates the maximum.
(iii) The spin statistics are controlled by the right hand slider and all the common cases are included. Note that, when one set of lines is completely missing (slider moved to zero) the pattern of line spacings is different from that when odd and even J are equally weighted. The first S line, S(0), is present but the first O line, O(1), is absent.
(i) Note that the gap between the Rayleigh line and the first rotational line is 6B (if all lines are present) and is 4B between successive lines and make sure that you understand the reasons. These are consequences of the ΔJ = ± 2 selection rule.
(ii) The first four values of the spin statistics are the same as for the infrared spectrum. Test the relative spacings for odd J: even J = 0:1 (right hand slider fully to the left); the first line is still at 6B but the spacing between successive lines has increased to 8B. Here the additional possibility, that occurs in oxygen, of even J lines being missing is included (right hand slider fully to the right). This happens because the oxygen nuclei are bosons but the ground state electronic wavefunction is antisymmetric. Verify that the first line is now at 10B not 6B while the spacing between successive lines is 8B just as for the case of odd J: even J = 0:1.
The interactive applet below calculates the infrared vibration rotation spectrum associated with a stretching vibration of a linear molecule. Click here for information concerning applets.
The calculation of the infrared spectrum is complete and includes the effects of centrifugal distortion, although these cannot be adjusted. If you download the programs the parameters of the control program can be changed to calculate any chosen spectrum for stretching of a linear molecule. Just set the parameter "control" to 1 and the remaining parameters are obvious.
The following are suggested "experiments" for the infrared spectrum.
(i) The B (lower) slider controls the value of B in the lower state and the B (upper) slider controls the value of the upper state B relative to B (lower). Leaving the other sliders at their initial setting vary these two sliders. You should be able to observe that the spacing of the lines is approximately 2B and that a difference between the upper and lower state Bs leads to a convergence of the lines in one branch and a divergence in the other. You should write out the formula for the lines to see why this is. The most common difference in the two B values leads to a the convergence being in the R branch. Note that the maxima in the P and R branches occur at a similar distance in cm−1 from the band origin (2000 cm−1) regardless of the value of B.
(ii) With the values of B lower and upper fixed vary the temperature and note how the maxima in the P and R branches move further from the band origin as the temperature increases. The reason for the maximum is that as J increases the increasing degeneracy (2J + 1) favours a higher population but the decreasing Boltzmann factor favours a lower one. The different rate at which these factors change generates the maximum. This gives a very useful means of estimating temperatures, especially in inaccessible situations such as in planetary atmospheres. If you keep the temperature fixed and increase B (lower) to a moderately high value you will realize that the discreteness of the lines makes it less and less accurate to determine temperature from the line of maximum intensity.
Almost any general book on spectroscopy will cover most of the topics above. There is an Oxford Chemistry Primer, Brown, Molecular Spectroscopy . Other suitable ones have been written by Whiffen, Banwell, Barrow, Hollis, Dixon. The books Molecular structure, and Chemical Consequences of Nuclear Spin, both by Wheatley, and very old, are useful for reading about structural determination, and bosons and fermions respectively.
Herzberg, Diatomic Molecules is more advanced but is extremely well written and is useful for reference, especially if you only read the sections in large print.
You ought to do the infrared vibration-rotation experiment.
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
Show that the most populated rotational level in a diatomic molecular gas at equilibrium at temperature T is given by:
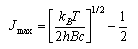
For the ground state of CN, the maximum occurs at J = 10 at 300
K. In a flame, it occurs at J = 27. Estimate the temperature of
the flame, indicating the likely uncertainty in your value. What assumptions
have you made regarding the molecular energy distribution in the flame?
Suggest a more accurate way of estimating the flame temperature,
supposing that you were able to measure the relative populations of several
rotational levels in CN.
The relative intensities of the R(0) and R(1) lines in an electronic transition in interstellar CN radicals were found to be 1 and 0.16 respectively. Given that the spacing of the lines is 7 cm-1, to estimate the interstellar temperature. Note that the intensity of a rotational line is given most accurately by
(J/+J//+1)exp(- BhcJ//(J//+1)/kT)
where J// and J/ indicate lower and upper rotational states respectively.
The rotational heat capacity curves of ortho (symmetric nuclear spin wavefunction) and para deuterium (I = 1) and HD are shown below.
(a) From the relative values of T at which CV is R/2 identify which sets of rotational levels are associated with ortho and para-D2. Give your reasons for this identification.
(b) Calculate the ratio of degeneracies of the first excited and ground states for the two forms of D2. By comparison with the behaviour of the heat capacity for a two level system (you will have to look this up), suggest reasons why there is a sharp maximum for ortho but not one for para-D2.
(c) The nuclear spin of D is 1. Write down the possible nuclear spin states for D2 and hence calculate the nuclear spin degeneracy of ortho and para-D2.
(d) Use the difference in in reduced masses between HD and D2 to determine the relative spacing between ground and excited states in HD and ortho-D2. Hence explain the appearance of the heat capacity curve for HD.
You will find it helpful to refer ahead to the rotational heat capacity applet in statistical mechanics.
Indicate whether the following molecules are spherical, symmetric, or asymmetric tops:
Sulphur trioxide, methane, sulphur tetrafluoride, sulphur hexafluoride, nitrogen trifluoride, ethylene, ethane, benzene, allene.
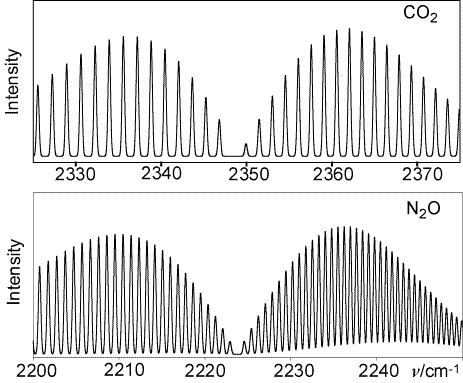
Infrared vibration-rotation bands of CO2 (top) and N2O are shown below. Describe in as much detail as you can the similarities and differences between the two bands.
Lines in the pure rotational Raman spectrum of oxygen are observed at 14.381, 25.876, 37.369, 48.855, 60.337, 71.809, 83.267, 94.712, 106.143, 117.555, 128.949 cm-1.
Assign the lines and use a graphical method to determine the ground state rotational constant and the bondlength of oxygen.
The pure rotational Raman spectra of benzene and deuterobenzene have been analysed to give the rotational constants 0.18960 cm -1 for C6H6 and 0.15681 cm-1 for C6 D6.
Determine the C-C and C-H bondlengths in benzene.
Three absorption lines of 12C 16O lie at 115.271201, 230.537974 and 345.795900 GHz.
(a) Assuming these to be the lowest frequencies and that D is small, suggest the initial and final level for each transition.
(b) Calculate B and D as accurately as possible.
(c) Infrared measurements on the transition to the v = 1 level give B1 = 57.11073 GHz. Using this value and B0 from (b) calculate B e and hence Ie
(d) Determine re for CO.
(a) Describe the normal modes of vibration of a linear symmetrical XY2 molecule and deduce, in terms of dipole moment and polarisablility changes, which of the modes are infrared and/or Raman active. How are the selection rules modified if the molecule is linear but unsymmetric, of the type XYY or XYZ?
(b) How do infrared vibration-rotation band contours and the degree of polarisation of Raman lines aid in distinguishing bond-stretching from angle bending frequencies in the vibrational spectra of linear molecules?
Interpret the observed infrared and Raman frequencies for the linear N
2O molecule given below:
| Frequency/cm-1 | Shape of infrared band | Raman |
| 2223.5 | PR branches | polarized |
| 1285.0 | PR branches | polarized |
| 588.8 | PQR branches | absent |