The Thomas Group - PTCL, Oxford

Statistical Mechanics - What you need to know

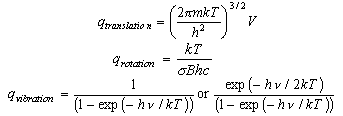
The basic assumption of statistical mechanics can be written in a number of ways.The simplest is

S = klnΩ

where Ω is the number of ways of arranging the system (number of configurations, etc.). This is a useful expression where it is necessary to relate entropy to disorder, e.g. residual entropies (questions 6 and 7 in Statistical mechanics-II) and number of ways of arranging atoms on adsorption sites (question 13), but it is not generally useful (or used) for deriving more complicated relations. It is sometimes referred to as the microcanonical ensemble.

The most important way of expressing the basic assumption (often referred to as the canonical ensemble) is

A = -kTlnQ

where A is the Helmholtz free energy and Q is the partition function for the whole system. This equation should be the starting point of most derivations. At this level it does not need to be derived or justified in any way.

The partition function Q is related to the molecular partition function q by

Q = q^N

for a solid, and

Q = q^N/N!

for a gas. The former applies to distinguishable molecules (they can be distinguished by their position in the lattice) and in the latter the N! allows for the molecules being indistinguishable. There are intermediate cases but these are normally treated specially.

You should learn the formulae for the molecular partition functions for translation, rotation of a diatomic molecule and vibration. These are

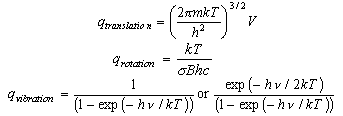
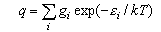
where B and ν are in cm^-1 and σ is the symmetry number (2 for a homonuclear diatomic). The alternative formula for q_vibration includes the zero point energy, i.e. it refers to the bottom of the potential well rather than to the energy at v = 0. There is generally no need to consider the effects of nuclear spin unless you are dealing with the H₂ molecule, in which case the partition function must be derived from the basic expression

where g_i is the statistical weight of the ith level and ε_i is its energy. The electronic partition function is usually 1 for molecules (notable exceptions are O₂ (³Σ_g^-, q_electronic = 3), NO (q_electronic = 2 + 2exp(-ε/kT))) but may have to be evaluated if there are low lying electronic states. It is not usually 1 for atoms because the electronic ground states of atoms often have several closely spaced levels (relative to kT).

To derive thermodynamic quantities from the basic assumption, A = -kTlnQ,

it is necessary to know the basic thermodynamic relations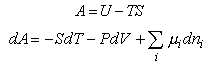

from which

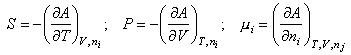
Note that the expression given here for μ is equivalent to the one that you are more familiar with, in terms of G. Finally, you should know that the equilibrium condition is

dA = 0 at constant T, V

To derive an expression for the entropy of a monatomic gas (Sackur-Tetrode equation) we start with the basic canonical ensemble equation and substitute q for a gas

A = -kTlnQ = -NkTlnq_trans + kTlnN!

The entropy is then

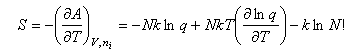
Writing the expression above for q as BT^3/2 gives

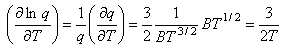
Using this and Stirling's approximation in the expression for the entropy gives

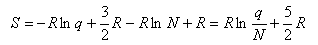
which, when the expression for q_trans is inserted, gives the Sackur-Tetrode equation for the entropy of a monatomic gas. To obtain the entropy of a diatomic gas it is necessary to add

Rlnq_rotation + Rlnq_vibration

to the Sackur-Tetrode equation. Note that the expression for the entropy of a solid is not the same as for a gas because the partition function Q does not have the N! factor.

Since both A and S are known, a useful expression for the internal energy can now be derived:

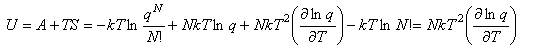
This expression for U is important and should be remembered. It should also be remembered that the heat capacity is defined by

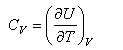
and hence the heat capacity can be obtained using statistical mechanics.

The chemical potential of a gaseous species can be written

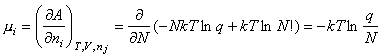
This can be used to obtain the statistical mechanical expression for the equilibrium constant, as follows. From conventional thermodyanamics we have

from which, when the stoichiometry condition is included (this is all similar to the derivation of ΔG = - RTlnK), we obtain

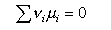
Substituting into the statistical mechanical expression for the chemical potential gives

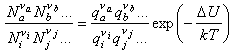
where a, b etc. refer to the reactants and i, j refer to the products, and ΔU₀ is the difference in the energies of reactants and products at T = 0 K. This appears in the equation because the energies in the expression for the partition functions must be referred to a common zero. For example, in the calculation of a vibrational partition function for a molecule with an additional energy U we would write

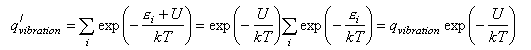
We now convert the N_i to concentrations by dividing by V

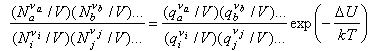
and use N/V = P/kT to obtain

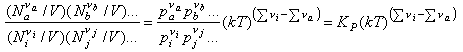
Hence

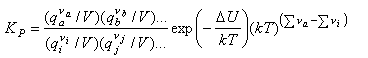
The term (kT)^Δν looks a bit complicated but it just represents the change in the number of molecules from reactants to products, e.g. it is 1/kT for the reaction of nitrogen and hydrogen to form ammonia, for which K_P is given by

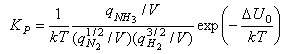
Note that q_trans contains the volume V and hence this cancels out in the calculation of an equilibrium constant by statistical mechanics.