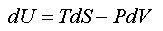
The first and second laws of thermodynamics can be written as
(1) The internal energy U is a state function,
(2) (a) The entropy S is a state function, (b) In an isolated system S is a maximum at equilibrium.
A combined mathematical statement of (1) and (2)(a) is
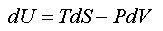
which, for convenience, we rearrange to
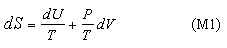
These equations apply to a single component. We now apply the second equation (M1) together with the condition (2)(b) to determine the conditions for equilibrium between two sub-systems within a single isolated system and this is done in the panel below.

Although the result, that temperature and pressure are uniform in the system at equilibrium, is not surprising, the method can now be extended to the more interesting situation of a two component system. First, we note that the use of the phrase state function is equivalent to stating that U is a perfect differential, i.e. that
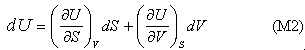
Other arguments, which have not been presented here, make the link between T and P and the two derivatives:
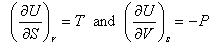 .
.
Equation (M2) only applies to a single component. For a two component system U will certainly depend on the amounts of each component present and so the complete expression for U should become
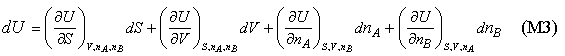
which, for convenience, we abbreviate as
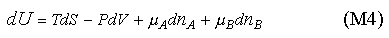
Equation (M4) can be rearranged in the same way as used to obtain (M1). We use the result in the panel below to establish the equilibrium conditions in a two component system, using the same method as for the panel above.

It is more convenient to have a definition of the chemical potential in terms of the Gibbs free energy G. The definition of G is
G = U + PV - TS
from which
dG = dU + PdV + VdP - TdS - SdT
Using equation (M4) we obtain
dG = VdP - SdT + mAdnA + mBdnB
By analogy with equations (M3) and (M4) mA is the same as
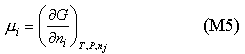
In a two component system the Gibbs free energy contains contributions from the free energies of the two pure substances and from the mixing. The contribution from the pure substance is just G/n where n is the number of moles of substance. The contribution from mixing varies with concentration. This contribution can be obtained in the ideal case by applying equation (M5) to equation (E3) (Entropy of Mixing). The result (derivation) gives a contribution to mA of RTlnxA. Because this result combines the two assumptions defining the ideal solution they can be replaced by the single definition of an ideal solution as one for which the chemical potentials of the components are given by
