These are a provisional set of problems. Their difficulty and the number of them will be reduced over the next week or so. You should treat the course as though it also includes the work in the lecture course Thermodynamics of Solutions done last term.
Many of the hints that you need are essentially included in a .
This asks multiple choice questions (you may need a calculator) and the quiz finishes when you have answered 15 questions correctly. However, you will not have access to the answers until you score better than 75%. It would therefore be sensible to make sure that your performance on the quiz is good before you do the problems.
1. The table below lists the electrostatic, induction and dispersion contributions to the intermolecular attractive potential energy for water and ammonia, calculated in each case for an intermolecular separation of 0.3 nm.
| - | Uel/kJ mol-1 | Uind/kJ mol-1 | Udisp/kJ mol-1 |
| NH3 | -6.2 | -0.9 | -12.9 |
| H2O | -16.1 | -0.9 | -5.3 |
(i) Use these data to estimate (a) the ratio of the dipole moments and
(b) the ratio of the polarizabilities for ammonia and water. Give an explanation
for which molecule has the larger polarizability.
[The ionization potentials of ammonia and water are 10.4 and 12.6 eV
respectively]
(ii) The quantities given in the table are calculated for 300 K; discuss
how these quantities will change with increase in temperature to 350 K and
explain the physical basis of any temperature dependence predicted.
(iii) How would the quantities change if calculated for a distance of
0.35 nm?
(a) Write down a form of virial equation for describing the relation between the pressure, temperature and volume of a gas. (b) The second virial coefficent B of a gas is related to the intermolecular potential U between two molecules at a distance r by
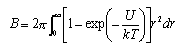
(i) Show that for molecules that behave like hard spheres of radius σ ( U = ∞ when r < σ, U = 0 when r > σ) the virial coefficient is given by B 0 = 2πσ3/3
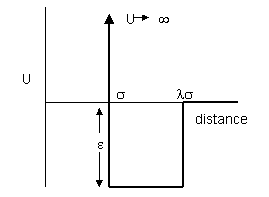
| (ii) For real molecules there is also
an attractive interaction. An approximate representation of the attraction
potential can be made using the square well potential shown on the right.
Show that the expression for the virial coefficient now becomes
(iii) The temperature at which N2 behaves like an ideal gas (the Boyle temperature) is 325 K. Given that the ratio λ is 1.58 for N2 use the value of the Boyle temperature to calculate the depth ε of the square well potential. |
|
(iv) Experimentally determined values of the second virial coefficient of N2 at lower temperatures are given below.
| T/K | 100 | 125 | 175 | 250 |
| B/cm3 mol-1 | -163.6 | -104.8 | -50.1 | -16.2 |
Using the value of ε and/or λ you have obtained in (iii) show that the square well potential accounts accurately for the data in the table above. Use the data to calculate σ.
CO2 is expanded from a vessel of volume V1 at a pressure P1 into a larger vessel of volume V2 to a final pressure P2. Given the virial equation
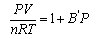
and that P2 is low enough for the gas to behave ideally, show that
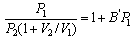
At 273 K the following values of P1 and P2 were obtained:
| P1 | 20 | 1 |
| P2 | 1.080 | 0.048 |
Calculate B', assuming that the gas behaves ideally at and below
a pressure of 1 atm.
At 693 K B' is zero while at 210 K it is -0.012 atm
-1 . Comment on the three values of B'.
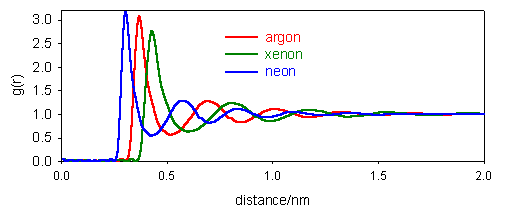
Describe what is meant by the pair distribution function of a liquid. How does it differ from the pair distribution functions of solids and gases?
(b) The pair distribution functions for the liquid states of Ne, Ar and Xe are shown in the diagram below. Comment on the general pattern of g(r) and estimate the distance between nearest neighbours in each case.
(c) The interaction between a pair of inert gas atoms is given by
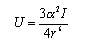
where the electronic polarizabilities α' and ionization potentials I of the inert gases are as given in the table below. Explain the origins of this formula and calculate the values of U for the three gases at the distance at which they are separated in the liquid, using the nearest neighbour distances you have estimated in (b).
| Inert gas | Ionization energy/kJ mol-1 | α'/nm3 |
| Ne | 2085 | 0.4 x 10-3 |
| Ar | 1524 | 1.6 x 10-3 |
| Xe | 1173 | 4.0 x 10-3 |
(d) Taking the entropy of vaporization of liquid xenon to be 80 J K -1 mol-1 and the boiling point to be 166 K, calculate the enthalpy of vaporization of Xe. By equating the enthalpy (H) and energy (U) of vaporization use your value of U for xenon to estimate the coordination number in liquid xenon.
(e) Applying the same approximations and assuming that the entropy of vaporization is the same for all three inert gases estimate the boiling points of Ar and Ne.
(f) What problems would arise if you tried to apply the same calculation to He?
5. (i) Explain what is meant by the term regular solution.
(ii) Write down expressions for the entropy of mixing when two components are mixed to form a regular solution.
(iii) Show how the enthalpy of mixing, ΔHmix, in a regular solution of two components, A and B, may be related to the pairwise interactions between its components, HAA, HBB and HAB, via an equation of the form
ΔHmix = βxAxB
where β depends on HAA, HBB and HAB.
(iv) For a regular solution, the first and second derivatives of ΔGmix with respect to mole fraction vanish at an upper critical solution temperature (UCST). Use your results from parts (ii) and (iii) to write an expression for ΔGmix in terms of x1. Evaluate the derivatives and hence show that
Tc = β/2R
(v) The excess free energy of mixing of an equimolar mixture of acetonitrile and CCl4 is 1190 J mol-1 at 450C. Assuming that the mixture obeys regular solution theory, calculate the UCST.
(i) The figure below shows a plot of the free energy of mixing, ΔGmix, for a two component system, over the full range of molar composition, xA = 0 → 1 and a range of temperatures.
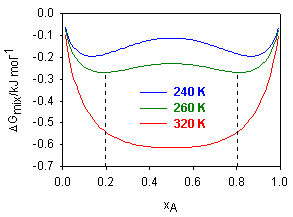
(a) Over what range of compositions will the mixture be immiscible when the temperature is 260 K?
(b) At this temperature, the mixture was found to behave as a regular solution. Write down expressions for ΔGmix, and (∂Gmix/∂xA)T in terms of xA; hence calculate the enthalpy of mixing of the two components at the composition xA = 0.1.
(c) Calculate the upper critical solution temperature of the mixture, assuming the solution remains regular up to this temperature.
6. Given that the Debye length is about 10 nm in aqueous 0.001 mol dm-3 KCl at room temperature, calculate its value in aqueous 0.01 mol dm-3 solutions of (i) KNO 3, (ii) CaCl2, (iii) Na 2SO4, (iv) CuSO 4 , (v) LaCl3.
The solubilities of a uni-univalent salt in an aqueous solution of sodium chloride (which had no ion in common with the salt) at 298 K were
| NaCl/mol dm-3 | 0 | 0.001 | 0.005 | 0.01 | 0.02 |
| Salt/mol dm-3 | 4.90 x 10-4 | 5.00 x 10-4 | 5.22 x 10-4 | 5.40 x 10-4 | 5.65 x 10-4 |
Calculate the solubility product of the salt and its activity coefficient in a saturated solution in water.
The degree of dissociation α of ethanoic acid, CH3CO2H, in aqueous solution at 298 K varies with concentration c in the following manner:
| c/mol dm-3 | 2.801 x 10-5 | 1.532 x 10-4 | 2.414 x 10-3 | 5.912 x 10-3 |
| α | 0.5393 | 0.2875 | 0.0829 | 0.054 |
Calculate the (thermodynamic) dissociation constant of ethanoic acid. How far do the data verify the Debye-Huckel theory?
9. The radius of gyration and second virial coefficient of a sample of polystyrene dissolved in cyclohexane were measured at a series of temperatures with the following results
| T/K | 305.7 | 307.2 | 311.2 | 318.2 | 328.2 |
| Rg/nm | 47.9 | 51.8 | 57.6 | 62.5 | 66.5 |
| B | -0.40 | -0.20 | 0.37 | 0.95 | 1.58 |
Estimate the unperturbed root mean square end-to-end distance (empirically) and the θ temperature in this solvent.
10. The intensity of X-rays scattered by a 50 mg cm-3 protein solution falls by a factor of 10 when κ ( = (4πsinθ)/λ) where 2θ is the scattering angle and λ is the wavelength) increases from 0.1 to 1.0 nm -2 . If the scattering obeys the law ln I = ln I 0 - κ 2 R 2/3, what is the radius of gyration of the protein?
11. Describe how the short range chemical structure of a polymer is related to its conformation in solution and derive an equation relating the mean square end-to-end distance of a random flight polymer to the number of formula units in a statistical segment.
The radius of gyration for poly(styrene) in cyclohexane at 310 K was found to be 6.2 nm for a molecular weight of 50k. Given that the length of the formula unit is about 0.3 nm estimate the number of formula units in a statistical segment.
12. (a) Explain what is meant by the radius of gyration of a polymer. How is it related to the end-to-end distance for a single chain polymer and what is its significance?
When κRg<<1 the intensity, I, of neutron scattering from a polymer molecule obeys the law I = I0exp(-κ 2 Rg 2/3) where I 0 is the incident intensity, κ is related to the angle of scattering, and R g is the radius of gyration. Two samples of amorphous polystyrene, A and B, each containing a small fraction of deuterium labelled polymer, gave the scattering data in the table below.
| κ/nm-1 | 0.1 | 0.2 | 0.3 | 0.4 |
| IA/arbitrary units | 0.776 | 0.365 | 0.103 | 0.018 |
| IB/arbitrary units | 0.474 | 0.023 | 1.48x10-4 | - |
Determine the radii of gyration of each of the polymers.
The molecular weights (Mn) of the two samples are 100k (sample A) and 400k (sample B). Comment on the relation between the two values you obtain.
14. The θ condition for a polymer in solution may be achieved by varying either the temperature of a single solvent or the composition of a mixed solvent. Comment on the factors involved.
Measurement of the osmotic pressure of a poly(isobutylene) sample in (a) cyclohexane and (b) benzene gave the following results:
| c/g dm-3 | 1 | 2 | 3 | 4 |
| Π/Pa(a) | 5.17 | 13.95 | 27.26 | 45.68 |
| Π/Pa(b) | 3.32 | 7.04 | 12.16 | 15.70 |
Determine the molecular weight and the second virial coefficient in each solvent. Comment on the results.
15. Measurement of the osmotic pressure Π (Pa) of a poly(styrene) sample in mixtures of dichloroethane (A) and cyclohexane (B) at 285 K in the A:B ratios given gave the following results:
| c/g dm-3 | 1 | 2 | 3 | 5 |
| Π/Pa(65:35) | 2.52 | 6.92 | 13.20 | 31.40 |
| Π/Pa(35:65) | 2.23 | 5.78 | 10.62 | 24.25 |
| Π/Pa(6:94) | 1.76 | 3.90 | 6.39 | 12.50 |
Determine the molecular weight of the polystyrene and the second virial coefficient in each mixture of solvents. Use your values for the second virial coefficient to decide which of the two solvents is the better solvent for poly(styrene).
16. (a) For a two component system the Gibbs isotherm is often written as dγ =-Γ 1RTdln a1 - Γ 2 RTdlna 2 where γ is the surface tension, a 1 and a2 are the activities of the two components, and Γ 1 and Γ 2 are the surface excesses of the two components. Show how this may be simplified and applied to estimate the relative surface excess of phenol at the two concentration limits at the surface of an aqueous solution from the following data taken at 293 K:
| [phenol]/mol dm-3 | 0.05 | 0.08 | 0.127 | 0.268 | 0.496 |
| γ/mN m-1 | 67.88 | 64.60 | 60.10 | 51.58 | 44.97 |
(b) Solutions of phenol in water are not ideal. A more accurate value of the surface coverage can be obtained by using the activity rather than the concentration of phenol. By using measurements of the partition of phenol between water and oil the activity of phenol was determined to give the table given below
| aphenol/mol dm-3 | 0.0485 | 0.076 | 0.121 | 0.241 | 0.407 |
| γ/mN m-1 | 67.88 | 64.60 | 60.10 | 51.58 | 44.97 |
Use this data to make a new plot of the Gibbs isotherm and hence obtain a more accurate value of the surface coverage at the limiting phenol concentration of 0.496 mol dm-3 .