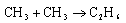
The problems below are based on some of the material is that covered in two lecture courses, Modern Liquid Kinetics and Interfacial Kinetics. Two useful books in the Oxford Primer Series are Cox, Modern Liquid Phase Kinetics and, to a lesser extent Fisher, Electrode Dynamics.
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
(a) Estimate the collision frequency of molecules (of RMM 18) in (i) a gas at atmospheric pressure and 300 K, and (ii) a gas with the same density as liquid water at 300 K. Use a collision diameter of 5 Å.
(b) Estimate the diffusion controlled rate constants for the reaction of two neutral particles in (i) hexane (ii) water at 300 K. Comment on the following approximate rate constants for the recombination of solvated electrons and cations in hexane (~ 1014 dm3 mol-1 s-1) and water (~ 1010 dm3 mol -1 s-1. The viscosities of hexane and water are 3.26 x 10-4 and 1.00 x 10 -3 kg m-1 s-1 respectively.
The observed activation energy for the radical recombination process
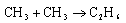
in solution is approximately 10-15 kJ mol-1. In the gas phase, the activation energy is close to zero. Comment. Explain why the reaction in solution is four times slower than might be expected on the basis of solvent viscosity.
(d) A much smaller concentration of biacetyl (butane-2,3-dione) is required to quench the fluorescence of naphthalene in solution in hexane than in glycerol (propan-1,2,3,-triol).
In solution the mechanism for a bimolecular reaction between species A and B may be written
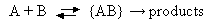
What is meant by the species {AB} appearing in this mechanism?
Derive an expression for the rate constant of a reaction in solution in terms of the elementary processes shown above. Hence explain under what conditions such a reaction would be expected to be diffusion-controlled.
The diffusion-controlled rate constant for a bimolecular reaction between species A and B in solution (expressed in dm3mol-1s-1) can be written as kD = 4000πrABDABNAf(U) where rAB is the encounter distance (expressed in m), DAB = DA + DB is the relative diffusion coefficient (in m2s-1) and f(U) is some function of the interaction potential energy, U, between the reactants, evaluated at the encounter distance. For reactions between neutral species, f(U) can be set to unity.
(a) A typical diffusion coefficient for a small molecule in aqueous solution is DA = 2.0 × 10-9m2s-1. Use this value to estimate the diffusion-controlled rate constant for a reaction involving neutral species, assuming an encounter distance of 0.5 nm.
(b) Diffusion-controlled rate constants typically decrease with increasing solvent viscosity and often have activation barriers (typically between 10 kJ mol-1 and 20 kJ mol-1). Comment on this observation.
For a reaction between ions in solution
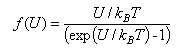
where the Coulomb potential can be written as
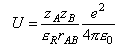
where zA and zB are the reactant charge numbers, εR is the relative permittivity, and e2/4πε0 = 2.307 × 10-28 J m.
(c) Sketch the variation of f(U) with U/kBT, and use it to explain qualitatively the effect charge has on the diffusion rate constant. Note that ex = (1 + x +..) for small x.
(d) Calculate f(U) for the reaction between solvated electrons and singly charged cations in hexane and in water at 300 K, given the relative permittivities of hexane and water are 1.89 and 78.5 respectively, and assuming an encounter distance of 0.5 nm. Comment on the result you obtain.
Comment on the following:
(a) For a number of ion-ion reactions in solution there exists a correlation between the entropy of activation, the volume of activation and the dependence of the reaction rate on pressure.
(b) For a series of electron transfer reactions it is sometimes possible to measure rate constants that decrease as the Gibbs energy of the reaction becomes more negative.
(c) Addition of an inert electrolyte accelerates some ion-ion reactions and decelerates others.
(d) In acid catalysed reactions addition of an inert electrolyte sometimes causes an increase in the rate of reaction.
(e) Estimate the encounter distance for the reaction of H+ and OH- in water at 300 K from the following data: diffusion coefficients, D(H+) = 9.1 x 10 -9 m2 s -1 , D(OH-) = 5.2 x 10 -9 m2 s-1 ; rate constant = 1.4 x 1011 dm3 mol -1 s-1. Comment on your answer.
(a) A simplified form of the Marcus theory expression for the rate of an electron transfer reaction in solution is
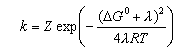
where Z is a constant for the solvent, ΔG0 the standard free energy of reaction and λ is a free energy of reorganization of the system in passing from reactants to products. Sketch how lnk is predicted to vary for different reactions as ΔG 0 alters from being slightly positive to being less than -λ. Explain the chemical reasons for the behaviour you have predicted.
(b) In a hypothetical photochemically induced electron transfer reaction in solution, a donor molecule D becomes excited to D* , which then transfers an electron to an acceptor A
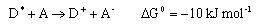
Charge neutralisation

is energetically more favourable. Assuming that the reorganization energy λ is 30 kJ mol-1, calculate the ratio k b/ka at T = 298 K on the basis of the expression for k above.
The molar conductivities (cm2 ohm -1 mol-1) of NaCl, CaCl 2, and LaCl3 at 298 K are tabulated as a function of concentration below:
| c/M | 0.0002 | 0.0005 | 0.001 |
| Λ(NaCl) | 125.2 | 124.5 | 123.7 |
| Λ(CaCl2) | 132.3 | 130.3 | 128.0 |
| Λ(LaCl3) | 139.0 | 135.0 | 130.0 |
Account for this concentration dependence and determine the limiting molar conductivities at zero concentration.
The limiting conductivity of the Cl- ion at this temperature is 66 cm2 ohm-1 mol-1. Calculate the limiting conductivity of the Na+ ion and compare it with the value of 38.7 cm2 ohm-1 mol -1 for the Li+ ion at this temperature.
The conductivities of both Li+ and Na + increase by 1.75 times between 298 and 328 K. Comment.
Discuss the data given below for conductivity measurements in water, pure sulphuric acid and liquid ammonia,
| - | H2O | H2SO4 | NH3 |
| viscosity/ g m-1 s-1 | 0.29 | 25 | 0.25 |
| conductivity/ohm-1 cm2 mol-1 | - | - | - |
| Na+ | 50 | 3 | 158 |
| K+ | 74 | 5 | 176 |
| HSO4- | 52 | 151 | - |
| H+ | 350 | 152 | 142 |
At applied voltages significantly far from the equilibrium electrode potential the current at a cathode varies with overvoltage η (η = E-E 0 according to the equation
logi = logi0 - ηα F/2.3RT
where α is often about 1/2. Explain briefly the origin of this equation.
The concentrations in the cathode compartment of a cell containing NaOH solution are such that at the mercury cathode the equilibrium potentials, E0 for sodium and hydrogen are respectively -1.87 and -0.83 V. For H2 and Na i 0 is 10-12 and 10-2 A cm-2 respectively. In each case α is close to 1/2. Calculate the ratio of sodium to hydrogen liberated at the cathode when it is operated at -2.0 V. Note that the sodium dissolves in Hg to form an amalgam which is kinetically stable under the conditions of hydrolysis.
What is meant by the term overpotential in electrochemistry, and how do overpotentials arise?
If an electrode is connected as an anode in an electrolytic cell, over a certain range of the overpotential η the current flowing, i, can be shown to be related to η by an equation of the form
i = i0exp{(1 - α) Fη/RT
where F is the Faraday constant. What interpretation is to be placed on the constant α in this equation? The following measurements were made at T = 298 K of current i as a function of η in a cell where the electrode was made positive
| i/10-5 A | 15.9 | 25.4 | 164.3 | 1063.4 |
| η/10-3 V | 75 | 100 | 200 | 300 |
How far are these data consistent with the simple expression, and what value of α do they predict?
Do you expect this equation to work at values of η of around 10 mV?
One more question to come. (a) Explain, without technical details, how a cyclic voltammogram is obtained.
(b) The figures below show typical cyclic voltammograms for `fast' (reversible) and `slow' (irreversible) single-electron reductions at an electrode surface.

What is meant by fast and slow electron transfer kinetics in the context of cyclic voltammetry? Comment on the different shapes of the two plots.
(c) Typical cyclic voltammograms are shown below for (i) two sequential, reversible 1-e- electron transfer reactions, (ii)an EC reaction with a fast chemical step (E designates an electron-transfer step and C a chemical step), (iii) an ECE reaction, (iv) a surface-bound electroactive species. Describe the features of the voltammograms that are characteristic of each process.