Where the question number is enclosed in a button, e.g.  , you can obtain help or comments about the question by clicking it.
, you can obtain help or comments about the question by clicking it.
There are three main topics.
(i) Electron spin resonance (electron paramagneic resonance, EPR). Especially important are hyperfine splittings by nuclear spins in aromatic radicals.
(ii) Time dependent quantum mechanics relating to Fourier transform NMR and two exchange (see applet in NMR tutorial material).
(iii) The quantum mechanics of the two coupled spin problem. You have already covered this in nmr and the applet showing the switch from AB to AX and the accompanying changes in the energy levels and the spectra should be looked at again ((see NMR. The quantum mechanics is exactly the same for AB, AX, EPR, with EPR generally corresponding to the AX extreme, except for the H atom in weak magnetic fields. You should be completely on top of this quantum mechanics and how it relates to the different spectral situations.
There are two OUP Primers, Nuclear Magnetic Resonance by Hore, and NMR: A Toolkit by Hore et al.However, there are several relevnt chapters in Carrington and MacLachlan, Principles of Magnetic Resonance, that are perfectly designed for this part of the course. It has the quantum mechanics and it covers EPR thoroughly.
Where the question number is enclosed in a button, e.g.  , you can obtain help or comments about the question by clicking it.
, you can obtain help or comments about the question by clicking it.
1. The allyl radical (CH2CHCH2) can be formed in the liquid phase by electron irradiation of cyclopropane.
(a) Use Huckel theory to construct the secular equations for the p molecular orbitals of the allyl radical.
(b) Determine the molecular orbital energies and the linear combination of atomic orbitals associated with them.
(c) Estimate the electron spin densities at each carbon atom of the neutral radical and show that the charge density arising from the p electrons would be uniform at each carbon atom in the radical cation.
(d) Use your results to predict the EPR spectrum of the neutral radical in solution.Compare them with the observed hyperfine coupling constants of 1.48 mT (2 protons), 1.39 mT (2 protons) and 0.41 mT (1 proton) and suggest possible reasons for any deviations.
2. (a) Sketch the hyperfine structure of the EPR spectra you would expect to obtain from the singly charged negative free radicals of (i) p-benzosemiquinone, (ii) benzene and (iii) cyclooctatetrene.
(b) Explain the appearance of the EPR spectrum of the 12CH3 methyl radical. In this planar radical the hyperfine coupling constant is directly proportional to the unpaired electron spin density in the p-orbital on the carbon atom. If the observed coupling in 12CH3 is 64.5 MHz, predict the EPR spectrum of the benzene negative ion 12C6H6.
(c) Explain why the EPR spectrum of the cation radical of the molecule shown below consists of 65 lines which can be explained in terms of just two hyperfine coupling constants.

3.The 9.25 GHz EPR (ESR) spectrum of the radical HO-CH-COOH in aqueous solution comprises four lines at field positions 3298.160±0.985mT, and 3298.160±0.725mT. Explain the appearance of this spectrum by means of an energy level diagram.
4. (a)(i) When naphthalene in solution in 1,2 dimethoxyethane, is reduced with potassium metal, a green coloured solution is obtained whose EPR spectrum is shown below. By considering the pattern of hyperfine splittings (some of which are indicated below) show that this specimen is consistent with the naphthalene radical anion.
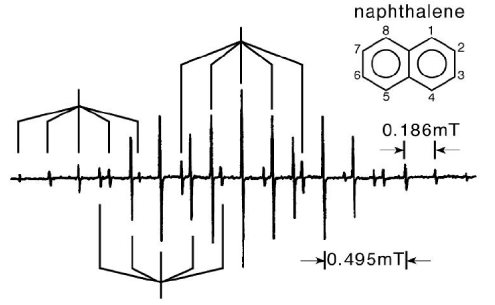
(ii) The ¹H hyperfine couplings of aromatic radical ions are given aproximately by the McConnell relation
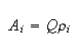
where ρi is the spin population at carbon i, A is the hyperfine coupling constant of the proton attached to carbon i and Qi is the hyperfine coupling for unit spin population on the carbon atom.
Discuss the mechanism of the hyperfine coupling between the unpaired electron abd the protons in aromatic radical ions.
(iii) The LUMO of naphthalene, as calculated by Huckel theory, is
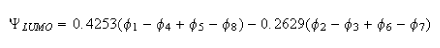
where the subscripts correspond to the numbering in the figure. Show that this molecular orbital accounts reasonably well for the observed hyperfine coupling constants of the naphthalene radical anion, and determine an average value for Q.
(iv) The hyperfine coupling constants for the anthracene radical anion in 1,2, dimethoxyethane are 0.274 mT (protons 1, 4, 5, 8), 0.151 mT (protons 2, 3, 6, 7) and 0.534 mT (protons 9, 10), Using your value of Q from (iii) estimate the spin populations at carbons 1,2 and 9 in the anthracene radical anion.
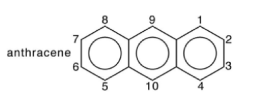
(v) The assignment of the three observed hyperfine splittings in the anthracene radical anion to particular groups of equivalent protons, as given in (iv), were obtained in part by deuteration of the anthracene molecule. Discuss how replacement of some of the protons in anthracene by deuterium could allow one to arrive at unambiguous assignments.
5. In a strong magnetic field, the spin levels of a radical containing an unpaired electron and two groups of equivalent magnetic nuclei are given by
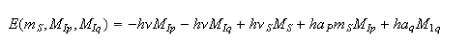
(a) Explain the meaning of all the terms in this equation and discuss the factors that determine νS, ap and aq.
(b) State the selection rules for EPR and obtain from the equation an expression for the allowed EPR transitions and hence explain why the EPR spectrum comprises
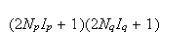
lines where Np and Nq are the numbers of the two types of nuclei.
(c) A polycyclic aromatic compound C13H10 is oxidized to form a radical C13H9 whose EPR spectrum comprises 28 lines representative of two different groups of equivalent 1H. Suggest a structure of the radical.
(d) An organic radical anion contains two different groups of equivalent nuclei and has an EPR spectrum consisting of 45 lines. Given that the molecule contains only carbon and hydrogen plus 4 nitrogen atoms, suggest a possible structure.
(e) There is an EPR technique called ENDOR (electron-nuclear double resonance) that effectively allows one to record the NMR spectrum of a radical. The selection rules for ENDOR are
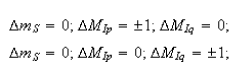
Using the equation above show that the ENDOR spectrum of a radical containing two groups of equivalent protons contains just four lines, whatever the values of Ip, Iq, Np and Nq. Comment on the possible advantages of ENDOR compared with EPR as a means of studying the magnetic properties of radicals.
6. (a) What is meant by a free induction decay in NMR?
(b) The free induction decay of an ensemble of identical nuclei with Larmor frequency ω can be written in complex form as
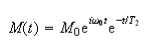
where the magnetisation My is given by the real part of the expression and T2 is the transverse relaxation time.
The NMR spectrum, I(ω), is obtained by Fourier transformation of M(t):
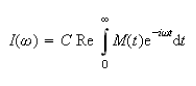
where C is a constant and `Re' represents the real part of the expression that follows.
Show that
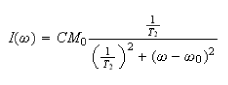
and hence that the full width at half maximum, Δν, of the peak is given by (c) How does the expression for Δν in (b) assist in the determination of rate constants in dynamic equilibria?
(d) The proton-decoupled 13C-NMR spectrum of liquid 2,3-dimethylbutane [(CH3)2CHCH(CH3)2] is shown below at temperatures of -100 oC and -180oC.
The relative peak areas and the peak separations (in Hz) are indicated. You may assume that integrated peak areas are proportional to the number of spins in the sample.
(i) Assign the NMR peaks in the spectrum acquired at -100 oC and explain why more peaks are observed in the spectrum at -180 oC than at -100 oC.
(ii) By carefully considering the different rotational conformers in 2,3-dimethylbutane, assign the peaks at -180 oC and determine the relative populations of the different conformers. (Note that not all the peaks are fully resolved.)
(iii) The linewidth of the peak labelled `A' at temperatures sufficiently low that chemical exchange is insignificant is ?v=71 Hz; at -178 oC, Δν = 125 Hz. Estimate the rate constant, k, at -178 oC for the exchange process you have identified in (ii) above and hence calculate the activation free energy, ΔG (b) The figure below shows four free induction decays. Two of them correspond to an NMR spectrum with a single line and two of them correspond to spectra with two lines of equal intensity.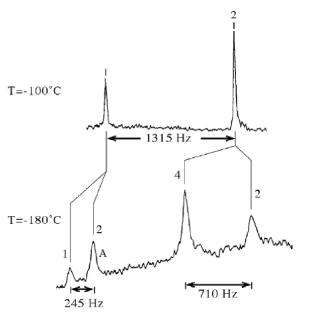
‡.
 (a) Explain in detail the principles of the measurement of a free induction decay and how it is related to the NMR spectrum.
(a) Explain in detail the principles of the measurement of a free induction decay and how it is related to the NMR spectrum.
(i) Identify which spectrum is which,
(ii) Determine the separation (in frequency) of the centre of gravity of each of the four spectra from the exciting line,
(iii) Determine the splitting (in frequency) of each of the two line spectra.