
(i) Absorption, spontaneous emission, and stimulated emission. Einstein coefficients for these processes.
(ii) The possible fates of a quantum of energy adsorbed by a molecule. These can be divided into four categories, emission of the energy from the same molecule, energy transfer to another molecule followed by emission, and either reaction of the starting molecule or of one to which the energy has been transferred.
(iii) Emission processes from the molecule itself: Fluorescence, phosphorescence, internal conversion, intersystem crossing and their measurement. The meaning of quantum yield and how it is determined. Discussion of the factors that influence the quantum yields of the different processes.
(iv) Simple discussion of electronic energy transfer and means for following it. Fluorescence quenching and the Stern-Volmer equation.
(v) Dissociation and predisssociation of the molecule absorbing the radiation.
(vi) Discussion of examples of lasers which operate using some of the processes above.
Use lecture notes and Wayne, Principles and Applications of Photochemistry for particular topics.
There are two relevant experiments, one on the dissociation energy of I 2 and the other on fluorescence and fluorescence quenching.
1. For a 3.7 x 10-3 M solution of naphthalene in hexane the peak of the first absorption band is at 301 nm. The intensity of light at this wavelength is reduced to 0.1 of its orginal value on passing through 1 cm of this solution. Obtain the molar absorption coefficient.
The width of the absorption band at half the maximum intensity is estimated to be 3000 cm-1. Assuming that the band can be represented approximately as triangular in shape, calculate the absorption coefficient and hence estimate the radiative lifetime of the S 1 state. The refractive index of hexane is 1.375. The measured fluorescence lifetime and quantum yield are 96 ns and 0.198 respectively. Comment.
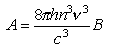
where B the absorption coefficient, is given by
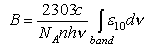
where a factor of 1000NA converts the mol dm-3 units of ε 10 to molecules cm-3 and the 2.303 convertsε10 to ε e. The refractive index n is also included in the formula for A. A is the radiative rate constant (= kF ))
2. The molar absorption coefficient for a compound is 3 x 10 4 dm3 mol-1 cm-1 at 313 nm, where the compound is photochemically bleached. The product does not absorb at 313 nm. A 1.5 x 10 -3 M solution of the compound in a 1 cm3 cell of 1 cm2 cross section was placed in the path of a light beam of 0.01 mW cm-2 at 313 nm. The absorbance decreased by 7 % of its original value in two hours. Obtain the quantum yield of the bleaching reaction.
3. In a solution of K3[Fe(C 2O4)3 ] the Fe(III) is reduced to Fe(II) on exposure to light. The quantum yield for Fe(II) formation at λ = 400 nm is 1.13 and the molar extinction coefficient (base e) at this wavelength is 594 cm -1 mol-1 dm 3 . A solution of concentration 0.006 mol dm -3 is contained in a cell of thickness 1 mm. The solution is irradiated for 20 min with light of λ = 400 nm and it is found that 3.4 x 10-6 of Fe(II) are formed. What is the intensity of light incident on the cell (measured in quanta s -1 )?
4. (a) A 10 cm thick sample of a 10-4 M solution of a fluorescent organic molecule X transmits 30 % of the incident radiation at λ = 333 nm (ν =30000 cm-1 ) corresponding to the peak of the absorption to the first excited singlet state. Calculate the molar extinction coefficient of X.
(b) In the absence of quencher, X possesses a fluorescence quantum yield of near unity for excitation at λ = 333 nm. Flash photolysis experiments show that the intensity of fluorescence, I f falls off after excitation in the following way:
| If/arb.units | 124 | 102 | 57.3 | 21.9 | 8.35 |
| t/ns | 1 | 2 | 5 | 10 | 15 |
Calculate the Einstein A coefficient (rate constant for radiative emission)
(c) Another molecule Y shows a peak intensity in its first absorption band similar to that of X. Both absorption bands of X and Y are roughly triangular in shape. However, the absorption band of Y is centred on ν = 20000 cm -1, and has a width twice that of X. Estimate the ratios of Einstein A factors for radiation from X and Y, and hence, from the result of (b) above, the A factor for the molecule Y.
(d) The measured half life for fluorescence of the molecule Y is 1 ns in a particular solution. Calculate the quantum yield for fluorescence of Y under these conditions. Give possible reasons for the occurrence of this value.
5. Light from a line of a mercury lamp is totally absorbed in a solution of potassium ferrioxalate, which decomposes with a quantum efficiency of unity at a rate of 10-7 mol s-1 . When the same light is used to investigate the fluorescence of a solution of Y in a cell 1 cm thick, the following results are found:
| [Y]/mol dm-3 | 0.1 | 0.01 | 0.001 |
| Total emitted intensity/quanta s-1 | 2.4 x 1016 | 2.4 x 1016 | 1.5 x 1016 |
Find values for the quantum efficiency of fluorescence of Y and the extinction coefficient of Y. When [Y] is 0.01 mol dm3 addition of chloride ion has the following effect:
| [Cl-]/mol dm-3 | 0 | 0.01 | 0.1 |
| Total emitted intensity/quanta s-1 | 2.4 x 1016 | 1.2 x 1016 | 2.16 x 1015 |
Comment on these values.
6. Propanone absorbs 313 nm radiation and exhibits a weak blue emission (380 - 470 nm) from a triplet state with a lifetime τ of 2 x 10 -4 s. Biacetyl does not absorb at 313 nm, but strongly quenches this triplet emission. Calculate the rate coefficient for this quenching process from the data below.
| ΦP/ΦQ | 1.21 | 1.43 | 1.65 | 1.84 | 2.02 |
| [Biacetyl]/mol dm-3 | 0.006 | 0.012 | 0.018 | 0.023 | 0.028 |
ΦP and ΦQ are the quantum yields for phosphorescence in the absence and presence of biacetyl.
7. Naphthalene contained in an alcohol-ether low temperature glass absorbs light at λ = 315 nm and two different emission spectra are observed. The quantum yields and lifetimes for the two emissions are (i) Φ = 0.3, τ = 3 x 10-7 s, and (ii) Φ =0.03, τ = 2.3. Estimate as many kinetic parameters as you can for the various processes occurring, assuming that no internal conversion or physical quenching occur. Explain qualitatively the magnitudes of the quantities that you obtain.
8. Show that the quantum yield Φ F , the radiative lifetime τ F and the observed lifetime τ in fluorescence are related by the equation
ΦF = τ/Φ F
where τ = 1/(kF + k NR) and kF is the radiative rate constant and kNR is the sum of rate constants for non-radiative processes depopulating the excited state. Quenching may be assumed to be absent.
When the fullerene C70, dissolved in a solid rare gas at 20 K is exposed to ultraviolet light, two distinct bands are seen. One has its origin at 15520 cm-1 and is approximately 10 times more intense than the second, whose origin is at 12588 cm -1. The lifetime of the stronger emission is 600 ps and its fluorescence quantum yield is 10-4 . The lifetime of the weaker emission is 50 ms. Identify the types of state involved in the emission processes and the transitions between them. Estimate the radiative lifetime for the stronger emission and comment on its value.
Indicate how values of the rate constants for other radiative and non-radiative processes in this system might be obtained.
9. (a) Explain why there is often a mirror image relationship between the absorption and fluorescence spectra of a molecule in solution. Under what conditions would such symmetry not be expected?
(b) Define what is meant by quantum yield.
A molecule is excited from its ground state to an excited singlet state in a flash photolysis experiment. Give expressions for the quantum yields of fluorescence ΦF and phosphorescence Φ P in terms of the rate constants for fluorescence k F , phosphorescence kP , and singlet-triplet intersystem crossing kISC .
Hence show that the rate constant for the disappearance of the excited singlet state is equal to kF/Φ F.
Assuming no chemical reactions take place, discuss the processes that could cause the sum of the two quantum yields (Φ F + ΦP to be smaller than the result obtained above.
(c) Continuous light (1.0 x 1016 quanta s -1 falls on a cell of thickness 1.0 mm containing a solution of a fluorescent compound B. The total fluorescence was determined as a function of the concentration of B.
| [B]/mol dm-3 | 0.0030 | 0.030 | 0.300 |
| Fluorescence/1015 quanta s -1 | 2.00 | 3.40 | 3.40 |
Determine the molar absorption (extinction) coefficient and the fluorescence quantum yield of B. Note that the fluorescence intensities at the two higher concentrations are identical.
10. The processes involved in the photochemical dimerization of an anthracene derivative in solution in ethanol are summarized below:
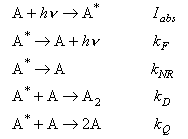
Give expressions for the quantum yields of the different processes in terms of the rate constants.
When the concentration of A is reduced to a level such that the quantum yields for dimerization and quenching are negligible, the fluorescence quantum yield is 0.218 and the intensity of fluorescence I expressed in arbitrary units, falls with time as follows:
| I | 0.97 | 0.62 | 0.40 |
| t/ns | 2 | 4 | 6 |
Calculate the rate constants kF and kNR.
At higher concentrations of A the quantum yield for dimerization Φ D varies with concentration of A as follows:
| FD | 0.037 | 0.081 | 0.105 | 0.121 | 0.137 |
| [A]/mol dm-3 | 0.01 | 0.03 | 0.05 | 0.07 | 0.1 |
Calculate the remaining rate constants kD and kQ. Comment on their values.
11. NO2 is irradiated with light of a particular wavelength in the presence of Xe buffer gas. The following elementary processes take place within the irradiated mixture:
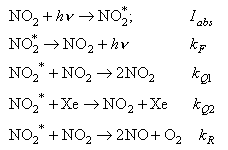
Derive an expression for the quantum yield of O2 .
The fluorescence lifetime τ was measured at 298 K by excitation with a pulsed laser to give the following data:
| τ/μs | 3.38 | 1.89 | 3.64 |
| [NO2]/molecules dm-3 | 3.2 x 1018 | 6.4 x 1018 | 3.2 x 1018 |
| [Xe]/molecules dm-3 | 1.6 x 1019 | 1.6 x 1019 | 0.8 x 1019 |
Use these data to determine the true fluorescence lifetime in its excited state.
12. Account for the following observations:
When a dilute solution of pyrene (a polynuclear, aromatic hydrocarbon) in ethanol is exposed to ultra-violet light, it emits a violet fluorescence. Sudden extinction of the ultraviolet source results in the near instantaneous (sub microsecond) extinction of almost all the fluorescence but, at high light intensities, in de-oxygenated solutions, the fluorescence decay also displays a delayed component.
In a concentrated solution, the violet fluorescence is replaced by an intense, sky-blue luminescence, which decays near instantaneously when the excitation source is extinguished.
When the concentration solution is cooled, becoming increasingly viscous and eventually forming a glass, the violet fluorescence returns as the sky-blue luminescence fades. Sudden extinction of the ultraviolet source again results in the near-instant loss of the fluorescence but, in the glassy solution, a red `afterglow' remains, decaying with a half life of about 1 s.