For comments and help click the button numbering the question.
Much of the material derives from the lecture course States of Matter. The main topics are:
(i) The form of the various possible interactions between a pair of uncharged molecules, particularly the Lennard-Jones potential (you do not need to know the details of the formulae for the various interactions),
(ii) The effect of intermolecular forces on gas phase properties, particularly the second virial coefficient,
(iii) Simple liquids and the description of some simple properties in terms of pair distribution functions and Lennard-Jones potentials,
To follow.
1. The HCl bondlength is 0.13 nm and its dipole moment is 1.8 D (1 Debye = 3.334 x 10-30 C m). Assuming a simple model in which the charges are localised on the atoms, calculate the partial charge on the chlorine atom.
2. The table below lists the electrostatic, induction and dispersion contributions to the intermolecular attractive potential energy for water and ammonia, calculated in each case for an intermolecular separation of 0.3 nm.
| - | Uel/kJ mol-1 | Uind/kJ mol-1 | Udisp/kJ mol-1 |
| NH3 | -6.2 | -0.9 | -12.9 |
| H2O | -16.1 | -0.9 | -5.3 |
(i) Use these data to estimate (a) the ratio of the dipole moments and
(b) the ratio of the polarizabilities for ammonia and water. Give an explanation
for which molecule has the larger polarizability.
[The ionization potentials of ammonia and water are 10.4 and 12.6 eV
respectively]
(ii) The quantities given in the table are calculated for 300 K; discuss
how these quantities will change with increase in temperature to 350 K and
explain the physical basis of any temperature dependence predicted.
(iii) How would the quantities change if calculated for a distance of
0.35 nm?
The second virial coefficent B of a gas is related to the intermolecular potential U between two molecules at a distance r by
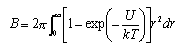
Show that for molecules that behave like hard spheres of radius σ ( U = ∞ when r < σ, U = 0 when r > σ) the virial coefficient is given by B 0 = 2πσ3/3
4. The Lennard-Jones potential for the interaction of two argon atoms may be written in the form
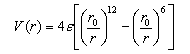
where r0 = 342 pm and ε = 1.712 x 10−21.
(a) Sketch the form of this potential and state which of the types of intermolecular force contribute to each term.
(b) Derive an expression for the force between two argon atoms at an arbitrary distance r.
(c) Calculate the radial position of the minimum in the potential and show that the well depth is equal to ε.
CO2 is expanded from a vessel of volume V1 at a pressure P1 into a larger vessel of volume V2 to give a total volume of V1 + V2 and a final pressure P2. Given the virial equation

and that P2 is low enough for the gas to behave ideally, show that

At 273 K the following values of P1 and P2 were obtained:
| P1 | 20 | 1 |
| P2 | 1.080 | 0.048 |
Calculate B', assuming that the gas behaves ideally at and below
a pressure of 1 atm.
Comment on why the value of the second virial coefficient is negative.
6. A van der Waals gas obeys the following equation of state:

where a and b are constants, assumed to be independent of p, V and T.
(a) Using the identity
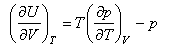
show that

where Um is the molar internal energy of the gas. Compare this result with that obtained for (dU/dV)T for a perfect gas and comment on the comparison.
(b) In the case of helium, the attractive forces are very weak and therefore a ≈ 0.
(i) Show that by setting a = 0, [d(pVm)/dp]T is independent of temperature for a van der Waals gas.
(ii) At 273 K the molar volume of helium at 100 bar is 0.011075 of its molar volume at 1 bar. By assuming the gas behaves as an ideal gas at 1 bar, determine a value for b and hence estimate the diameter of a helium atom.
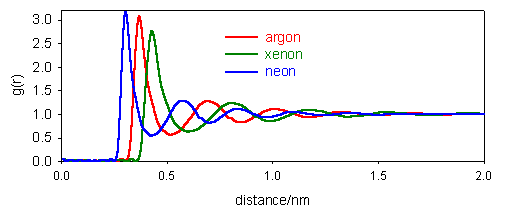
7. The pair distribution functions for the liquid states of Ne, Ar and Xe are shown in the diagram below.
(a) Comment on the general pattern of g(r) and estimate the distance between nearest neighbours in each case.
(b) How would you expect the pair distribution functions of solids and gases to differ from that for a liquid?
(c) The interaction between a pair of inert gas atoms is given by
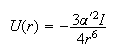
where the electronic polarizabilities α' and ionization potentials I of the inert gases are as given in the table below. Calculate the values of U for the interaction between a pair of atoms for each of the three gases at the distance at which they are separated in the liquid, using the nearest neighbour distances you have estimated in (a).
| Inert gas | Ionization energy/kJ mol-1 | α'/nm3 |
| Ne | 2085 | 0.4 x 10-3 |
| Ar | 1524 | 1.6 x 10-3 |
| Xe | 1173 | 4.0 x 10-3 |
(d) Taking the entropy of vaporization of liquid xenon to be 80 J K -1 mol-1 (Trouton's Rule) and the boiling point to be 166 K, calculate the enthalpy of vaporization of Xe. Assuming that the enthalpy (H) approximately equals the energy (U) of vaporization, use your value of U for xenon from (c) to estimate the coordination number in liquid xenon.
(e) Applying the same approximations and assuming that the entropy of vaporization is the same for all three inert gases estimate the boiling points of Ar and Ne.
8. The molecular weight of CHCl3 is 119
and its density is 1.48 g cm-3. Estimate the mean
separation between the molecules in the liquid (assume simple cubic packing
of spheres).
Calculate the relative energy contributions at this distance of the dipole-dipole
(rotationally averaged), dipole-induced dipole, and dispersion interactions
between two molecules. For CHCl3 α
0 ' = 8.1 x 10-30 m
3 , I = 106 J mol-1
, and μ = 1 D. Take T = 293 K and ε = 1.
9. The diffusion coefficient for methane in carbon tetrachloride has been measured to have the following values: D = 2.05 x 10−9 m2 s−1 at 273 K and D = 2.89 x 10−9 m2 s−1 at 298 K. Determine the activation energy associated with the diffusion process and the root mean square distance travelled in 1 s in both cases.
10. At 298 K the mean square displacement in water of latex spheres of radius 0.212 μm is measured to be 128 x 10−12 m2 in a time of 90 s. Use the Stokes equation to estimate the viscosity of water at 298 K.
11. Show that the increase in surface area when the radius of a sphere changes from r to r + dr is equal to 8πrdr, and give an expression for the work done in bringing about such an increase in terms of the surface tension γ.
Show that the total inward force on a spherical air-filled cavity in a liquid (i.e. a bubble) is equal to

where pout is the external pressure on the cavity. By balancing this force against the force due to the internal pressure, pint, show that

Hence calculate the pressure differential of ethanol across the surface of a spherical droplet of radius 220 nm at 293 K, at which temperature the surface tension γ = 22.39 mN m−1.