For help click the button numbering the question.
1(a) Explain what is meant by the pair distribution function of a liquid.
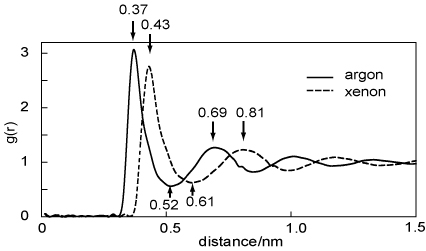
(b) The pair distribution functions, g(r), for the liquid states of Ar and Xe are shown in the diagram below. Comment on the main features of the two distributions (distances marked are in nm).

(c) The energy of interaction, E(r), between a pair of inert gas atoms separated by a distance, r, is given approximately by
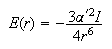
where the electronic polarizabilities α' (in appropriate units) and ionization potentials I of Ar and Xe are as given in the table below. Calculate the values of E for the two elements at the distance at which they are separated in the liquid.
| Inert gas | I/kJ mol−1 | α'/nm3 |
| Ar | 1524 | 1.6x10−3 |
| Xe | 1173 | 4.0x10−3 |
(d) The energy of vaporization, ΔU, of liquid xenon is 13.3 kJ mol−1. Use the value of E for xenon from part (c) to estimate the coordination number in liquid xenon.
(e) For an equimolar mixture of Ar and Xe the internal energy of mixing, ΔmixU, is given approximately by zβ/4 where z is the mean coordination number and
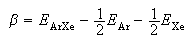
where EAr and EXe indicate interactions between identical molecules and EArXe indicates the interaction between argon and xenon. An accurate estimate of EArXe is that it equals −(EArEXe)1/2. Taking z to be 12, calculate the energy of mixing, ΔmixU, of equimolar argon and xenon.
The radial distribution gOH and 4πr2gOH are shown for ice (blue), water at 273 K (purple) and superheated water at 473 K (red) below.
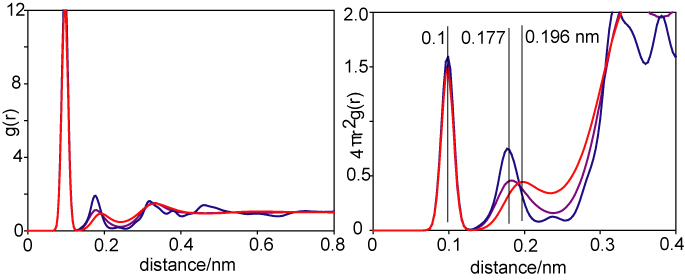
(a) What is the average hydrogen bond length (O-O distance) in the three situations shown?
(b) Assuming that each oxygen in ice is hydrogen bonded to exactly four other oxygens, estimate the number of intact hydrogen bonds in water at 273 K and at 473 K, given that the heights of the second peak in the distributions shown on the right above are respectively 0.75, 0.46 and 0.45 for ice, water at 273 K and water at 473 K.
(c) The enthalpy of fusion of ice is 6 kJ mol−1. Use this value together with your answer from (b) to estimate the average strength of a hydrogen bond (assume that this does not change between ice and water and that the coordination number for water molecules is about 4).
(d) Use the value from (c) and the mean number of hydrogen bonds per water molecule to estimate how much hydrogen bond energy is lost when water boils. The difference between this value and the observed latent heat of vaporization of water of 40.6 kJ mol−1 can be attributed to dispersion forces between water molecules. Using a coordination number of four estimate the mean disperion forces between a pair of water molecules in liquid water.
3. The solubility of trinitrotoluene in benzene at different temperatures is
| x | 0.279 | 0.382 | 0.493 | 0.622 |
| T/K | 303 | 313 | 323 | 333 |
where x is the mole fraction of trinitrotoluene. Assuming that the solutions are ideal, calculate ΔHfus and Tfus for trinitrotoluene.
The solubility of monoclinic sulphur at 298.3 K in various solvents (benzene, diethyl ether, ethyl bromide, ethanol) is always 1.28 times that of rhombic sulphur. In these solvents sulphur is known to be present only as S8 molecules. By equating the equations for the chemical potential of the two forms of sulphur in solution using the Henry's law limit, find ΔG for the change of monoclinic to rhombic sulphur at 298.3 K. Which of the two forms is more stable at this temperature?
5. At 300 K the surface tension of solutions of the surfactant C12H25(OC2H4)2OH in water as a function of its concentration is well accounted for by the equation
dγ/dlnc = − 13720c/(1 + 106c)
where the units of γ and c are N m-−1 and M respectively.
Use the Gibbs equation to calculate the surface excess (Γ) of the surfactant at a concentration of 3.0x10-5 M, and hence calculate the area per molecule at the surface.
6. For a two component system the Gibbs isotherm is often written as dγ =-Γ 1RTdln c1 - Γ 2 RTdlnc 2 where γ is the surface tension, c 1 and c2 are the concentrations of the two components, and Γ 1 and Γ 2 are the surface excesses of the two components. Show how this may be simplified and applied to estimate the relative surface excess of phenol in the concentration ranges of (a) 0.05 to 0.08 and (b) 0.268 to 0.496 mol dm-3 at the surface of an aqueous solution from the following data taken at 293 K:
| [phenol]/mol dm-3 | 0.05 | 0.08 | 0.127 | 0.268 | 0.496 |
| γ/mN m-1 | 67.88 | 64.60 | 60.10 | 51.58 | 44.97 |
Given that the cross section of a phenol molecule is about 0.4 nm2 estimate what fraction of the surface is covered by phenol at the higher of the two concentration ranges. Suggest an explanation for the low value that you should obtain.
7. State the relation between the concentration, c, of a non-ionic surfactant in solution in water and the surface tension, γ, of the solution (Gibbs equation).
The variation of surface tension with concentration, dγ/dc, of three non-ionic surfactants of general formula C12H25(OC2H4)mOH (designated C12Em) at concentrations, csat, where the surface is saturated, and at 298 K, is given in the table below.
| Compound | (dγ/dc)/N m-1 mol -1 dm3 | csat x 105/mol dm-3 |
| C12E3 | -381 | 3 |
| C12E6 | -88 | 8.5 |
| C12E12 | -46 | 12.5 |
Use the Gibbs equation to calculate the surface excess of each surfactant at saturation. Comment on the values you obtain.
(i) Explain what is meant by the term regular solution.
(ii) Write down expressions for the entropy of mixing when two components are mixed to form a regular solution.
(iii) Show how the enthalpy of mixing, ΔHmix, in a regular solution of two components, A and B, may be related to the pairwise interactions between its components, HAA, HBB and HAB, via an equation of the form
ΔHmix = βxAxB
where β depends on HAA, HBB and HAB.
(iv) For a regular solution, the first and second derivatives of ΔGmix with respect to mole fraction vanish at an upper critical solution temperature (UCST). Use your results from parts (ii) and (iii) to write an expression for ΔGmix in terms of xA. Evaluate the derivatives and hence show that
Tc = β/2R
(v) The excess free energy of mixing of an equimolar mixture of acetonitrile and CCl4 is 1190 J mol-1. Assuming that the mixture obeys regular solution theory, calculate the UCST.
(i) The figure below shows a plot of the free energy of mixing, ΔGmix, for a two component system, over the full range of molar composition, xA = 0 → 1 and a range of temperatures.
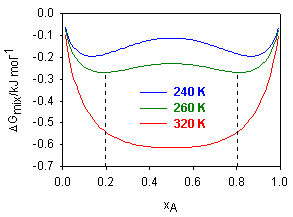
(a) Over what range of compositions will the mixture be immiscible when the temperature is 260 K?
(b) At this temperature, the mixture was found to behave as a regular solution. Write down an expression for ΔGmix in terms of xA. Obtain the condition for a minimum in ΔGmix and, by substituting into this expression the numerical values of x at one of the minima, obtain a value for the mixing parameter, β. Hence calculate the enthalpy of mixing of the two components at the composition xA = 0.1.
(c) Calculate the upper critical solution temperature of the mixture, assuming the solution remains regular up to this temperature.