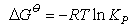
(i) It is most important to understand the concept of chemical potential, which is widely used in the equations for chemical equilibria. You need to understand two aspects of it, for which there are some accompanying notes, The first is the contribution of entropy of mixing to the free energy of a mixture. The second is the notion of chemical potential as the driving potential for chemical and physical change.
(ii) You should be able to derive the equations defining the equilibrium constant, Kp, and relating changes in Kp with temperature to the enthalpy of a chemical reaction. You should learn the following equations by heart:
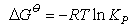
and
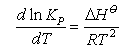
See Introduction to Thermodynamics
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
0.2889 g N2O4
was introduced to an evacuated vessel of volume 500 cm
3 . After equilibration the total pressure inside
was 161.0 mmHg at 298 K and 181.0 mmHg at 308 K. Find ΔH
O for the reaction
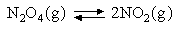
2. The following data refer to the reaction
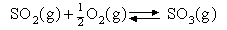
| T/K | 801 | 852 | 900 | 1000 | 1105 | 1170 |
| KP | 31.3 | 13.8 | 6.55 | 1.86 | 0.63 | 0.36 |
Calculate ΔHO over this
temperature range and comment on any assumptions you may make. What is
the value of ΔGO and
of Δ SO at 1000 K?
The standard Gibbs free energy of formation of NH
3(g) is -16.49 kJ mol-1
and the standard enthalpy of formation is -46.11 kJ mol
-1 . Assuming that ΔHO
f is independent of temperature calculate the equilibrium
constant for
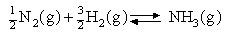
at (a) 298 and (b) 1000 K. Then find (c) the temperature at which the equilibrium constant = 1 and (d) the amounts of (i) N2 , (ii) H2 and (iii) NH3 present when 1 mol NH3 is allowed to come to equilibrium at this temperature and 1 atm pressure.
Between 400 and 500 K the standard free energy change for the gas phase reaction
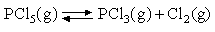
is given by:
ΔGO =
83680 - 14.52ln(T/K) - 72.26 (T/K) J mol
-1
Calculate (a) KP, (b) ΔS
O and (c) ΔH
O for the reaction at 450 K. Assuming all
species to behave ideally, calculate (d) the degree of dissociation
of PCl5 when 0.01 mol PCl5
is introduced into a 1 dm 3 vessel at
450 K.
5. Starting from the relationship between ΔG
O and KP
, the equilibrium constant in terms of partial pressures, show how
K P varies with temperature.
Determine ΔHO and Δ
SO at 1000 K for
the reaction
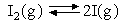
from the following experimental measurements of KP :
| T/K | 900 | 1000 | 1100 | 1200 | |
| KP | 3.94 x 10-4 | 3.03 x 10-3 | 1.70 x 10-2 | 6.72 x 10-2 |
Comment on the likely validity of any assumptions you make.