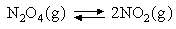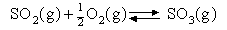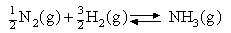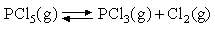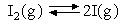Try the following:
(i) Set the energy slider at a low value, say 50 cm−1 and vary the temperature. Note how at low temperature there are almost no molecules being excited. This is the quantum effect; the available energy (kT) is far too small to excite molecules to the upper level. Note that at high temperature the populations of the two levels are tending to equality. Vary the temperature slowly between the two limits and note that the temperature at which the largest number of excitations occur corresponds to the maximum in the heat capacity. The heat capacity is zero at both high and low temperatures because there are no changes in population with temperature at these limits.
(ii) Keeping the temperature constant, vary the spacing (energy) between the two levels and note that the temperature for the heat capacity to be a maximum increases directly with energy. Pick a value of the heat capacity, then change the energy to a new value. Verify that you can adjust the temperature to recover your starting value of the heat capacity.
(iii) Examine the effect of changing the degeneracy ratio. By following the changes in population as you do this, see if you can come up with a verbal explanation of why the maximum value of the heat capacity is sensitive to this degeneracy ratio.
The second applet calculates the heat capacity associated with a single vibrational motion (it could be either the vibrational heat capacity of a diatomic molecule or part of the contribution to the Einstein heat capacity of a solid).
The applet calculates the heat capacity, internal energy and entropy (on the left) for the set of equally spaced vibrational energy levels shown on the right. As the temperature is varied (using the middle slider) the corresponding heat capacity is marked with a circle, the relative populations of the levels are shown in green on the right, and the relative changes in the number of excitations between the states are shown as the width of the blue arrow connecting the two states. You can vary the vibrational energy with both the slider on the left and by a multiplicative factor by the slider on the right. A further feature is that examples of molecules with the vibrational heat capacity on display are shown in the right hand box when the energy is set within 50 cm−1 of their known vibrational energies.
Try the following:
(i) The heat capacity curve for a set of uniformly spaced vibrational levels is a universal function (always the same shape). You can show this by changing the scale lever on the right. This multiplies the spacing and the temperature scale by the same factor. When the scale is changed the heat capacity curve remains exactly the same, i.e. doubling the vibrational energy is exactly cancelled by doubling the temperature. Note that this is not the case for the internal energy and the temperature.
(ii) Vary the temperature and note how the population of the levels changes. At low temperature the situation is the same as for the two level heat capacity, i.e. for a small rise in temperature there is a negligible change in population. The change in population from the ground to the first excited state is a maximum just below the temperature at which the heat capacity approaches its classical value, i.e. this point is similar to the peak in the two level case. The difference from the two level situation is that, as the temperature is further increased, energy can continue to be drawn into the system by populating the higher levels.
(iii) Note the variation of the internal energy U, which starts at 0 and then rises to its classical value of RT and of the entropy, which is the integral of C/T. If you find these applets useful you may find it useful to look at two further applets on rotational heat capacities and heat capacities of solids. The first applet here is also shown in slightly more complex form in the second year statistical mechanics.
Atkins, Physical Chemistry. See also Gasser and Richards, Introduction to Statistical Mechanics.
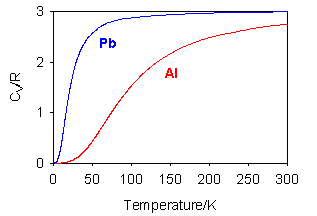
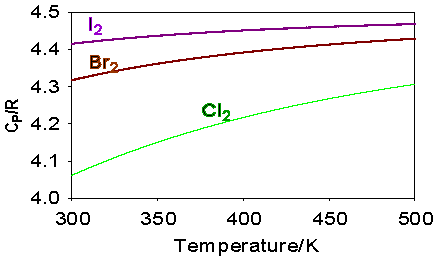
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it. The heat capacities of aluminium and lead are shown in the figure below. The heat capacities of gaseous iodine, bromine and chlorine as a function of temperature are compared in the figure below. Explain the differences.
Assuming that the equipartition principle holds for all possible motions estimate the value of ΔCV for each of the reactions below (these are the same as in the 5 problems in Equilibria). Convert these to values of ΔCP and deduce how ΔH varies with temperature in each case.
How would these predictions be altered if correct allowances for non-classical behaviour of the vibrations were included in the estimate of ΔCV?
The inert gases all have heat capacities, CP of 5/2R at room temperature, but their entropies are very different. Look up the values of the entropies of argon and xenon at about room temperature and suggest a qualitative explanation for the difference.
Bibliography
Problems
(i) Explain the differences between the two substances.
(ii) Deduce which of the two metals has the larger entropy at room temperature (a) by considering the number of accessible states in each case (using S = klnΩ) and (b) by using the relationship between S and heat capacity.