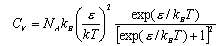
As well as doing the problems below, you should revise the problems that you were given in the second year and revise the basic theory of statistical mechanics..
A proportion of the work covered here forms part of the Solids and Surface Lecture Course, viz. heat capacities of solids, heat capacities of electrons in solids, and derivation of the Langmuir isotherm.
The main topics are the heat capacities of solids (Debye and Einstein models), heat capacities of electrons in metals, the Langmuir isotherm, and Schottky defects.
An applet designed to help you understand some of the concepts of the heat capacity associated with vibrations in solids is shown below (Click here for information concerning applets; the relevant filenames, if you wish to download them, are respectively tutorials/statmech/EinsteinEtc.jar and tutorials/statmech/EinsteinEtcAppletJ.html). You can access other applets showing the two level heat capacity problem, the vibrational heat capacity of a diatomic gas and the rotational heat capacity of a diatomic gas.
The applet calculates the heat capacity, energy or entropy (on the left) for the energy level distribution shown on the right. The results for both Einstein and Debye models are shown so that you can compare them. The sliders on the right allow you to switch between heat capacity, energy and entropy, and between normal temperatures (T axis) and low temperatures (T3 axis). Values of the Debye cut-off for various solids are also shown when they are close to the slider value of the cut-off.
Try the following:
(i) Note that whatever the temperature the two models can be adjusted to be very similar, each with different values of their frequencies (the value of the Debye cut-off is obviously always larger than the Einstein frequency).
(ii) The large difference between the two models shows up at low temperatures. Use the extreme right hand slider to switch to low temperatures. The Debye heat capacity varies linearly with T3 at low temperatures and this closely resembles actual experimentl heat capacities. The T2 extrapolation is very useful for extrapolating measurements to low temperatures. The Einstein model fails very badly at low temperatures and you may find it difficult even to get the Einstein curve on the screen. Values of fundamental constants Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it. 1. The heat capacity of CD4 in a clathrate
has been measured to be 4.3 R at 200 K. An infrared band at 96 cm
-1 may be assigned to a rattling motion of the Use the following data for aluminium to plot a graph of its heat capacity, CV, as a function of temperature. Discuss the shape of this graph and the origin of the temperature variation in terms of the properties of a typical solid. To what extent is the form of the function applicable to other solids?
CD
4 in the cage. In the gas phase CD4
has two degenerate fundamental vibration bands close to 1000 cm
-1 and two close to 2000 cm-1
. Suggest an explanation for the observed value of the heat capacity
at 200 K and indicate the likely form of the heat capacity curve in the
temperature range 65 to 200 K.
T/K
20
30
50
75
100
150
250
400
CV/R
0.0297
0.0998
0.4208
1.0074
1.5319
2.1873
2.6884
2.8982
The Debye cut-off frequency for aluminium is 279 cm−1. Assuming that the Debye cut-off frequency depends only on the mass of the atoms estimate the heat capacities of silver and lead at 30 K (the atomic masses are Al 27, Ag 108 and Pb 207).
The observed values of the heat capacities of silver and lead at 30 K are respectively 0.5R and 2.0R. Suggest possible reasons for the disagreement with your estimates.
(a) The heat capacity of many metallic solids has a low temperature behaviour that obeys the equation
Cv = γT + αT3
Explain the origin of the two terms on the right hand side of the equation.
(b) Experimental heat capacity data for potassium are given in the table below:
| T/K | 0.3379 | 0.4805 | 0.5661 | 0.7155 | 0.8332 | 0.9334 | 1.013 |
| C/mJ K-1 mol -1 | 0.7962 | 1.292 | 1.659 | 2.458 | 3.310 | 4.083 | 4.899 |
Use graphical means to determine the values of the two constants γ and α in the equation from part (a).
(c) Similar measurements on rubidium and caesium gave values of α that were respectively 11.4 and 31.4 mJ mol−1 K−4. To what extent can these changes be explained in terms of the different masses of the three species (atomic weights of K, Rb and Cs are respectively 39, 85 and 133)?
(d) The values of γ were found to be 2.41 and 3.20 mJ mol−1 K−2 respectively. Account for the differences of these values from each other and from that for potassium in terms of the expected variation of the Fermi levels of the three metals.
The torsional motion of the methyl group in solid nitromethane at low temperatures can be approximated by a two-level quantum system with degeneracies g0 = g1 = 4 and an energy level spacing of Δε = ε1 - ε0 = 0.5 cm−1.
(a) Write down an expression for the molecular partition function of this two-level system.
(b) Obtain an expression for the molar internal energy Em(T) of the system and sketch the behaviour of Em(T) as a function of T.
(c) Show that the heat capacity of the system is given by
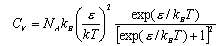
Discuss the behaviour of CV,m(T) in the limits (i) kBT << 1 and (ii) kBT >> 1.
(d) Without doing a detailed calculation, write down what you would expect to find for the molar entropy of the system, Sm(T), in each of the two limiting regimes specified in part (c).
(e) Speculate briefly on why a paramagnetic catalyst, such as O2, might be needed to achieve thermal equilibrium between the two levels.
(a) Explain why the entropy S associated with binding N immobile atoms at M sites is
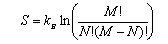
(b) A zeolite sample contains M cubic cavities of side d (connected by pores of negligible volume) into which atoms may be adsorbed with an adsorption energy . Show that the partition function of the N atoms adsorbed into the sample at temperature T is given by
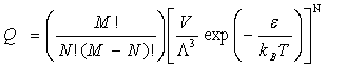
where
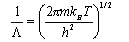
Hence show that the Helmholtz free energy of the adsorbed gas is
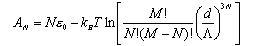
(c) The chemical potential is related to the Helmholtz free energy by
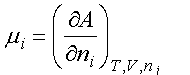
Obtain an expression for (i) the chemical potential of the adsorbed atoms and (ii) the chemical potential of N atoms of an ideal gas. By equating them, show that
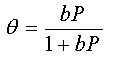
where
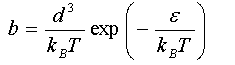
(d) A fractional occupancy of 0.1 is obtained at an argon pressure of 0.1 atm. at T = 200 K and at 0.2 atm. at 250K. Obtain values for ε and d.
6. The enthalpy of formation of a Schottky defect pair in a 1:1 ionic crystal is 10−19 J.
(i) Calculate the equilibrium fractional concentration, xs, of Schottky pairs at temperatures of 300 K and 1000 K, assuming xs << 1. (ii) Calculate the enthalpy change, the entropy change and the Gibbs free energy change of the bulk crystal which occurs when these defects form at 1000 K.