(i) Everything that you did in Kinetics in the first year is important and you should start by reviewing that and doing any problems that you failed to do then. The first two problems below are revision problems.
(ii) It is also important to revise the expressions for the equilibrium constant in terms of partition functions, which you did last term in Statistical Mechanics.
(iii) Review simple collision theory and its limitations. This is best done in terms of potential energy surfaces for reactions. It is also useful to examine the differences between collision and reaction cross sections, illustrating your discussion with examples,.
(iv) Transition state theory. The idea of the reaction coordinate as a separable motion. The use of the statistical mechanical expression for the equilibrium constant in terms of partition functions to derive an explicit formula for k(T).
(v) Comparison of the full derivation of transition state theory in (iv) with the thermodynamic formulation. Entropies of activation.
(vi) Comparison of transition state theory with collision theory. Application in the Arrhenius equation and to kinetic isotope effects. Deviations from Arrhenius behaviour. Quantum mechanical tunnelling.
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
The rate of the elementary gas phase reaction
CH + O2 → products
was determined using flash photolysis techniques under conditions where the molecular oxygen concentration was in large excess over that of the CH radical.
(i) Obtain an expression (in integrated form) for the time dependence of the CH radical concentration under these conditions.
(ii) The CH radicals were monitored as a function of time using the technique of laser induced fluorescence. The relative fluorescence intensity, I, proportional to CH concentration, is given in the table below at different times, t.
| t/10−6 s | 20 | 30 | 40 | 50 | 60 | 70 |
| I | 0.230 | 0.144 | 0.088 | 0.050 | 0.033 | 0.020 |
Verify that the kinetics are first order, and determine the pseudo-first order rate constant for the reaction.
In the above experiments the molecular oxygen concentration was 8.8 x 1014 molecules cm-3. Calculate the bimolecular rate constant for the reaction.
(iv) Derive an expression for the half-life of a bimolecular reaction when the two reactant concentrations are equal. What would be the half-life of the CH radicals if the O2 and CH concentrations were initially both equal to 5 x 1012 molecules cm-3, but conditions were otherwise unchanged?
In a study of the reaction of methyl radicals with ethanal vapour a substance CH3X, which decomposes with first order kinetics, is used as a source of methyl radicals. A mechanism that is consistent with the observed products is
CH3X → CH3 + X(inactive)
CH3 + CH3CHO → CH4 + CO + CH3
CH3 + CH3 → C2H6
By applying the steady state approximation derive an expression for the rate of formation of methane in terms of the concentrations of ethanal and CH3X. The rate of production of methane varies with the concentration of CH3X in the following manner:
| [CH3X]/arbitrary units | 5 | 10 | 20 | 50 | 100 |
| dCH4/dt/arbitrary units | 7.24 | 10.49 | 14.49 | 22.91 | 32.40 |
Show that this data is consistent with the mechanism above. How would the rate of formation of methane be expected to depend on the ethanal concentration?
How does the form of the potential energy surface linking products with reactants influence the distribution of excess energy in the products of an exothermic reaction?
What is meant by (a) a collision cross section σC, and (b) a reaction cross section σR?
How, in principle, is a thermal rate constant k for a reaction at a specific temperature obtained from the reaction cross section.
One theory suggests that σR varies with reactant translational kinetic energy ET according to the equation
σR = σR0(ET - E0)/ET
where σR0 is a constant and E0 is the threshold energy for reaction. The reaction
K + HCl(v) → KCl + H
is slightly endothermic for v = 0. The following data were obtained for the reaction cross section σR at different energies:
| ET/kJ mol-1 | 8 | 12 | 20 | 30 |
| σR/nm2 | 0.0033 | 0.0108 | 0.017 | 0.020 |
Estimate the threshold energy for reaction from the data. Vibrational excitation to v = 1 in HCl increases σR much more than the equivalent amount of energy in translational excitation. What qualitative conclusion can you draw about the shape of the potential energy surface?
(a) For the reaction A + BC → AB + C, show how transition state theory predicts that the pre-exponential factor of the rate constant should either be proportional to T−1/2 or temperature independent depending on the geometry of the transition state.
(b) Lindemann theory predicts an expression of the following form for the dependence of the rate of the unimolecular decomposition of substance A on concentration of an inert diluent [M].
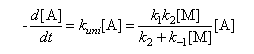
based on applying the steady state approximation to the reaction scheme
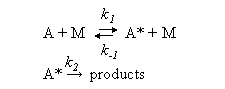
Show that on the basis of this model kuni falls to one half of its limiting high pressure value (k∞) when [M] = k∞/k1. Explain why values of k1 determined from this equation are generally much larger than predicted from simple collision theory.
(c) Explain why the rates of many radical-radical recombination reactions in the gas phase at low pressure show third order kinetics, and why the rates decrease with increasing temperature.
(d) In the reaction of HCl with K, (ΔH = 4 kJ mol−1) laser excitation of HCl to v = 1 (requiring 34.5 kJ mol−1) increases the reaction rate by a factor of 100, whereas increasing the average thermal energy of the reactants by the same amount through heating of the gases only increases the reaction rate by a factor of 10. The majority of the excess energy of this reaction is partitioned directly into translational energy of the products. Discuss what can be inferred from this data about the potential energy surface of the reaction.
The thermodynamic formulation of transition state theory for a gas phase bimolecular reaction may be written
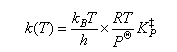
(a) Discuss briefly the origin of the factor kBT/h appearing in this expression.
(b)(i) The activation energy of a reaction is defined
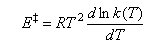
Use this equation, together with equation (1), and the van't Hoff equation
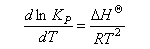
to show that
E ‡ = ΔH ‡O + 2RT
(ii) Hence show that the Arrhenius A-factor for a gas phase bimolecular reaction can be written as
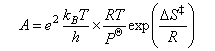
where RT/PO is typically expressed in units of dm3 mol−1.
(iii) Briefly explain what is meant by the terms ΔS ‡O and ΔH ‡O appearing in the above equations.
(c)(i) Simple collision theory yields the following expression for the Arrhenius A-factor, expressed in dm3 mol−1 s−1
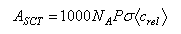
where <crel> = (8kBT/πμ)1/2 is the mean relative speed of the reactants (in m s1), σ is the collision cross-section (in m2), and P is the steric factor. Taking P = 1, and making reasonable estimates for a typical collision cross-section and relative speed at 300 K, estimate Asct.
(ii) Use your estimate, together with equation (2), to determine a simple collision theory value for ΔS ‡O at 300 K.
(iii) Account for the sign of ΔS ‡O obtained in (c)(ii). Explain why ΔS ‡O values derived from experimental kinetic data for bimolecular reactions in the gas phase are often more negative than the simple collision estimate, but are rarely less negative.
Theoretical expressions for the rate constant of a bimolecular elementary reaction step include the Eyring equation from transition state theory:
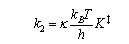
and the collision theory result:
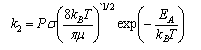
(a) Explain the significance of the terms P, κ, K‡, σ and μ in the above expressions.
(b) For what type of reaction are the predictions of the two theories identical, with P and κ equal to unity? Obtain the specific form of the Eyring equation, in terms of the partition functions, for this type of reaction.
(c) Express the rate constant for the radical reaction
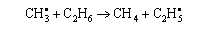
in terms of the molecular partition functions. Hence deduce how the pre-exponential factor for the radical reaction should depend on temperature. (Assume that all vibrational partition functions are unity)
(d) When the experimental activation energy (50 kJ mol−1) and the gas-kinetic collision cross sections are used, a P factor of 0.01 is found necessary to reconcile the collision theory result with results for the radical reaction. Explain why this factor is significantly less than one.
(a) Discuss the physical interpretation of the symbols σ, <c> and E0 in the simple collision theory expression for the rate coefficient of a bimolecular reaction,
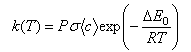
(b) The steric factor P can be calculated using transition state theory, which gives the rate coefficient of a bimolecular reaction A + B → products as
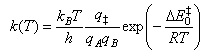
State the physical assumptions that lead to this expression, and provide one example of a situation where these assumptions might be expected to break down.
(d) Given that q‡, qA and qB are molecular partition functions per unit volume, the translational contributions to which can be written as (e.g.)
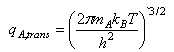
show that in the hypothetical case of a reaction between two hard spheres the transition state theory rate coefficient reduces to the simple collision theory result with P = 1, E0 = ΔE0‡, and
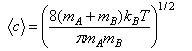
(e) Hence deduce that the steric factor for a reaction between two molecules A and B that proceeds via a linear transition state is given by
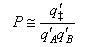
where the translational contributions are absent from the primed partition functions q‡/, qA/ and qB/ and the rotational contribution is also absent from q‡/. Noting that qvib ≈ 1 per vibrational degree of freedom and qrot ≈ 10 per rotational degree of freedom at room temperature, estimate the steric factor for (i) a reaction between an atom and a diatomic molecule, and (ii) a reaction between two diatomic molecules, assuming that the transition state is linear in both cases. Comment on the results you obtain.
(a) Consider the following gas phase reactions:
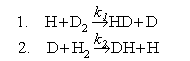
Estimate the ratio of the rate constants k2/k1 at 300 K using the vibrational wavenumbers given below. Assume that the effect of isotopic substitution is limited to changes in the zero point energies of reactants and transition states, and that the transition states are linear.
| - | H2 | Transition state 1 | Transition state 2 |
| stretch (cm−1 | 4395 | 1762 | 1773 |
| bend (degeneracy = 2)(cm−1) | - | 694 | 870 |
(b) For the reaction of an atom X with a diatomic molecule Y2
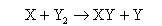
proceeding through a linear transition state, Transition State Theory gives
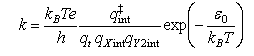
where qXint and qY2int are the partition functions for the internal modes (rotational, vibrational, electronic) of the reactants and qt is related to the masses of the reactants by
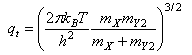
Outline the origin of the expression for k, comment on the assumptions involved, and explain the meanings of the symbols qint‡ and ε0.
(c) Show that the expression for k in (c) leads to the following equation, stating and justifying the assumptions and approximations used.
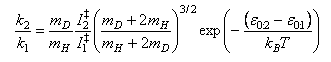
The 1,2 subscripts refer to the two reactions in (a) and I‡ denotes the moment of inertia of the transition state.
(d) Hence obtain a revised estimate of k2/k1 at 300 K. (I1‡ = 4.02 x 10−47 kg m2, I2‡ = 3.95 x 10−47 kg m2; the relative atomic masses of H and D are 1 and 2 respectively).
(e) The experimental value of k2/k1 is 14 at 300 K. Why is this value larger than predicted by Transition State Theory?