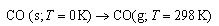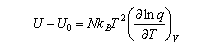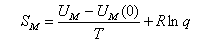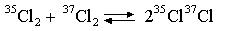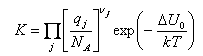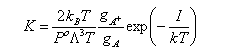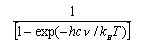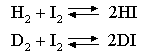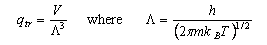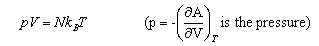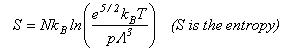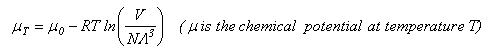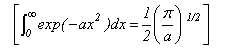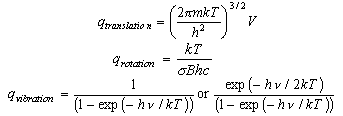
As well as doing the problems below, you should revise the work on heat capacities that you were given in the first year and some of the problems set in Vibrations and Rotations.
The basic assumption of statistical mechanics can be written in a number of ways. The simplest is
S = klnΩ
where Ω is the number of ways of arranging the system (number of configurations, etc.). This is a useful expression where it is necessary to relate entropy to disorder, e.g. residual entropies and number of ways of arranging atoms on adsorption sites (see Third Year Statistical Mechanics), but it is not generally useful (or used) for deriving more complicated relations. It is sometimes referred to as the microcanonical ensemble.
The most important way of expressing the basic assumption (often referred to as the canonical ensemble) is
A = -kTlnQ
where A is the Helmholtz free energy and Q is the partition function for the whole system. This equation should be the starting point of most derivations. At this level it does not need to be derived or justified in any way.
The partition function Q is related to the molecular partition function q by
Q = qN
for a solid, and
Q = qN/N!
for a gas. The former applies to distinguishable molecules (they can be distinguished by their position in the lattice) and in the latter the N! allows for the molecules being indistinguishable. There are intermediate cases but these are normally treated specially.
You should learn the formulae for the molecular partition functions for translation, rotation of a diatomic molecule and vibration. These are
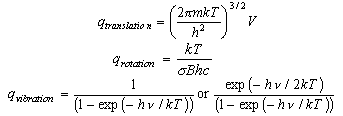
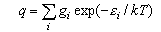
where gi is the statistical weight of the ith level and εi is its energy. The electronic partition function is usually 1 for molecules (notable exceptions are O2 (3Σg-, qelectronic = 3), NO (qelectronic = 2 + 2exp(-ε/kT))) but may have to be evaluated if there are low lying electronic states. It is not usually 1 for atoms because the electronic ground states of atoms often have several closely spaced levels (relative to kT).
To derive thermodynamic quantities from the basic assumption, A = -kTlnQ,
it is necessary to know the basic thermodynamic relations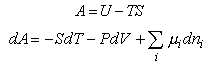
from which
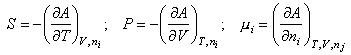
dA = 0 at constant T, V
To derive an expression for the entropy of a monatomic gas (Sackur-Tetrode equation) we start with the basic canonical ensemble equation and substitute q for a gas
A = -kTlnQ = -NkTlnqtrans + kTlnN!
The entropy is then
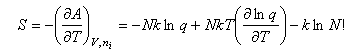
Writing the expression above for q as BT3/2 gives
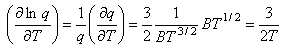
Using this and Stirling's approximation in the expression for the entropy gives
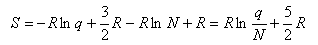
which, when the expression for qtrans is inserted, gives the Sackur-Tetrode equation for the entropy of a monatomic gas. To obtain the entropy of a diatomic gas it is necessary to add
Rlnqrotation + Rlnqvibration
to the Sackur-Tetrode equation. Note that the expression for the entropy of a solid is not the same as for a gas because the partition function Q does not have the N! factor.
Since both A and S are known, a useful expression for the internal energy can now be derived:
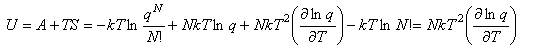
This expression for U is important and should be remembered. It should also be remembered that the heat capacity is defined by
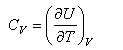
and hence the heat capacity can be obtained using statistical mechanics.
The chemical potential of a gaseous species can be written
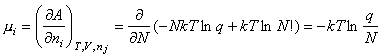
This can be used to obtain the statistical mechanical expression for the equilibrium constant, as follows. From conventional thermodyanamics we have
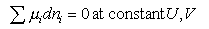
from which, when the stoichiometry condition is included (this is all similar to the derivation of ΔG = - RTlnK
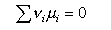
Substituting into the statistical mechanical expression for the chemical potential gives
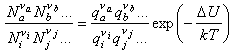
where a, b etc. refer to the reactants and i, j refer to the products, and ΔU0 is the difference in the energies of reactants and products at T = 0 K. This appears in the equation because the energies in the expression for the partition functions must be referred to a common zero. For example, in the calculation of a vibrational partition function for a molecule with an additional energy U we would write
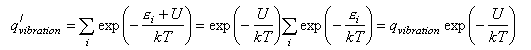
We now convert the Ni to concentrations by dividing by V
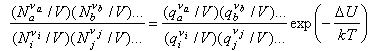
and use N/V = P/kT to obtain
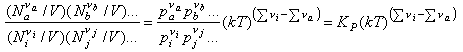
Hence
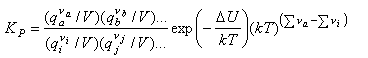
The term (kT)Δν looks a bit complicated but it just represents the change in the number of molecules from reactants to products, e.g. it is 1/kT for the reaction of nitrogen and hydrogen to form ammonia, for which KP is given by
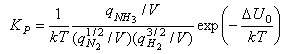
Note that qtrans contains the volume V and hence this cancels out in the calculation of an equilibrium constant by statistical mechanics.
To help you understand some of the concepts,two applets are shown below (Click here for information concerning applets; the relevant filenames, if you wish to download them, are respectively tutorials/statmech/twoLevelHeatCap.jar and tutorials/statmech/twoLevelHeatCapAppletJ.html for the two level system and tutorials/statmech/rotHeatCap.jar and tutorials/statmech/rotHeatCapAppletJ.html for the rotational heat capacity). The first one is a slight advance on one in the first year work and shows how the heat capacity, internal energy and entropy of a two level system vary with temperature, energy and degeneracy of the upper of the two levels.
The applet calculates the heat capacity, energy and entropy (on the left) for the pair of energy levels shown on the right. As the temperature is varied (using the middle slider) the corresponding heat capacity is marked with a circle, the relative population of the two levels is shown in green on the right, and the relative number of excitations from the ground to the excited state is shown as the width of the blue arrow connecting the two states. As well as adjusting the energy gap between the two levels and the temperature, you can also vary the ratio of the degeneracy of the upper to that of the lower state.
Try the following:
(i) Set the energy slider at a low value, say 50 cm−1 and vary the temperature. Note how at low temperature there are almost no molecules being excited. This is the quantum effect; the available energy (kT) is far too small to excite molecules to the upper level (more accurately, almost no change in population is necessary to change the Boltzmann distribution to that appropriate for a higher temperature and hence negligible energy is needed to raise the temperature). Note that at high temperature the populations of the two levels are tending to equality. Vary the temperature slowly between the two limits and note that the temperature at which the largest number of excitations occur corresponds to the maximum in the heat capacity. The heat capacity is zero at both high and low temperatures because there are no changes in population with temperature at these limits.
(ii) Keeping the temperature constant, vary the spacing (energy) between the two levels and note that the temperature for the heat capacity to be a maximum increases directly with energy. Pick a value of the heat capacity, then change the energy to a new value. Verify that you can adjust the temperature to recover your starting value of the heat capacity.
(iii) Examine the effect of changing the degeneracy ratio. By following the changes in population as you do this, see if you can come up with a verbal explanation of why the maximum value of the heat capacity is sensitive to this degeneracy ratio.
(iv) Note that for this two level system the energy and the entropy approach constant limiting values at high temperature. What are the values of the two limits? The second applet calculates the heat capacity associated with rotation of a diatomic molecule.
The applet calculates the heat capacity and internal energy (on the left) for the set of rotational energy levels shown on the right. As the temperature is varied (using the middle slider) the corresponding heat capacity is marked with a circle, the relative populations of the levels are shown in green on the right, and the relative changes in the number of excitations between the states are shown as the width of the blue arrow connecting the two states. You can vary the rotational constant B with the slider on the left. The heat capacity is very sensitive to the spin statistics and the slider on the right allows you to select a number of spin combinations.
Try the following:
(i) The spacing of rotational energy levels is approximately quadratically dependent on the quantum number J and the degeneracy increases with J. This leads to some important differences between the temperature dependences of rotational and vibrational heat capacities. The first is seen clearly at the starting settings of the applet. There is a small maximum in the heat capacity just before the behaviour becomes fully classical. This is because the system behaves almost like a two level system with a high degeneracy ratio. Vary the temperature in the region just below this point and watch the changes in population of the energy levels. They reflect this near-two level behaviour very clearly.
(ii) The near-two level becomes much more marked for certain spin statistics. Examine the effects for the various ortho and para hydrogen and deuterium situations. Note that the "equilibrium" curves are somewhat hypothetical in that they assume equilibrium flipping of the nuclear spins. However, the amplitude of the maximum in the curve can always be explained by the combination of the degeneracy ratio of the first two levels and the ratio of the spacing between the second two levels and that between the first two levels.
(iii) Note how the increasing degeneracy of rotational levels leads to a completely different pattern of occupation compared with that for vibrations (see first year applet of vibrational heat capacities) Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it. Click for Values of fundamental constants The rotational energy levels of a (heteronuclear) diatomic molecule are given by EJ = BhcJ(J+1), with B the rotational constant such that θ = Bhc/kB is the characteristic rotational temperature.
(a) Explain why the fraction of molecules found in the rotational energy levels specified by the quantum number J is
where qrot is the rotational partition function.
(b) Write down the expression for qrot and, by transforming the sum to a suitable integral, obtain qrot in the high-temperature limit. (c) To a first approximation the intensity of a rotational absorption transition from J → J' is determined by f(J). Explain briefly why this is so, and show that the line with maximum spectral intensity (J = Jmax) corresponds to
(d) The Stokes branch of the pure rotational Raman spectrum of the (heteronuclear) molecule consists of approximately equally spaced lines separated by 9.8 cm−1. Identify which rotational transition has maximum intensity at a temperature T = 298 K.
The heat capacity of CD4 in a clathrate
has been measured to be 4.3 R at 200 K. An infrared band at 96 cm
-1 may be assigned to a rattling motion of the A molecule has two low-lying non-degenerate energy levels separated
by energy ε. Write down an expression for the partition function of
the molecule and hence, or otherwise, derive an expression for the internal
energy, U. and plot the variation of CV with the
ratio ε/kT. Because of the rotation of the ammonia groups solid Ni(NH3
)6I2 has an
anomaly in its low temperature heat capacity CV
as shown by the data below:
Show that these data are consistent with the two level heat capacity equation
given above and estimate ε. By making an approximate extrapolation of CV
to zero at the low and high temperature ends of the anomaly estimate
the entropy change over the temperature range 0 to 1.5 K. Comment on the behaviour of CV in this system
and on the value of the entropy change across the anomaly. In terms of the canonical partition function Q = Q(N,V,T), the internal energy and Helmholtz free energy are given respectively by U = NkBT2(dlnQ/dT)N,V and A = −kBTlnQ.
(a) For a gas of independent particles, show that the entropy S is given in terms of the molecular partition function q by
where lne = 1. Stirling's approximation is lnN! ≈ NlnN - N for N >> 1.
(b) By considering an atomic gas, and neglecting the electronic degrees of freedom, show that the translational contribution to S may be expressed in the form
where m is the relative atomic mass, and C is independent of the chemical identity of the
gas.
(c) Assuming that only the ground and first excited electronic states are thermally accessible, show that the electronic contribution to the entropy is
where β = 1/kBT, g0 and g1 are degeneracy factors and ε is the energy of the excited electronic state relative to the ground state.
(d) Calculate the electronic contribution to the molar entropy of NO at T = 298 K. The energy separation between the ground and first excited electronic state of NO is 121 cm−1, and
kBT/hc = 207.2 cm (e) Obtain an expression for the rotational contribution to the entropy of NO.
(f) The total standard molar entropy of NO at T = 298 K is known to be Sm At Ttr = 61.6 K, CO undergoes
a solid state phase transition from an α-phase (T<T
tr) to a β-phase, with an associated latent heat Δ
Htr = 633 J mol -1
. Thermodynamic data for the temperature dependence of the isobaric
specific heat of the α-phase are given below; while C
P for the β -phase is approximately constant at 50.9 J
K-1 mol -1 . The
solid melts at T m = 68.1 K with Δ
H m = 835.5 J mol -1
; in the liquid phase C P = 60.4 J
K -1 mol -1 , and
is again independent of temperature. The boiling point is T
b = 81.6 K, with ΔH vap
= 6040 J mol -1, and C
P for the gas phase has the value predicted by classical
equipartition applied to the translational and rotational degrees of freedom
alone.
Using the above data, determine the entropy change associated with At normal pressure and T = 298 K, statistical mechanical calculations
show the molar entropy of CO to be Sm
(298) = 197.9 J K-1 mol-1
. Deduce the molar entropy of solid CO at T = 0, and explain
the microscopic origins of the value you obtain. 6. (a) The internal energy of a gas is related to the molecular partition function q and the number of molecules N by
where U(0) is the internal energy at absolute zero.
(i) Show that if q is proportional to Tz, then U - U(0) = zNkBT.
(ii) Comment on this result in the context of the translational, rotational and vibrational motion of diatomic molecules.
(b) The molar energy of a gas is given by
Account for the following approximate differences in molar entropies (in JK−1 mol−1) at 300 K:
(i) S(Xe) - S(Ar) = 15
(ii) S(DI) - S(HI) = 6
(iii) S(D2) - S(H2) = 14
(iv) S(35Cl37Cl) - S(35Cl2) = 6
Explain why the equilibrium constant for the reaction is 4 at 298 K. Evaluate the entropy changes at 298 K which occur when (a) one mole of 35Cl2
and one mole of 37Cl2
, each at one atmosphere, are mixed, without reaction, at a total
pressure of 1 atmosphere, (b) this mixture is then allowed to come to equilibrium. 8. Statistical mechanics gives the following result for the equilibrium constant K (= KP) of a gas phase reaction:
(a) Consider the thermal ionization of an atomic species A,
A → A+ + e−
with ionization energy I. For both A and A+, you need retain only the lowest energy electronic state (2S+1)L arising from the appropriate ground electronic configuration; the difference in energy between the spin-orbit components (J) of these states may be neglected.
(b) Show that the equation for this equilibrium may be expressed as
where Λ(T) is the de Broglie wavelength of the electron, and gA+ and gA denote respectively the degeneracies of the A+ and A electronic ground states.
See statistical mechanics formulae for formula for translational partition function. (c) Calculate K at T = 4000 K for the thermal ionization of carbon atoms (I = 1086 kJ mol-1)
(d) In assuming Boltzmann statistics, the above result for K effectively treats the electrons as classical particles. This is valid only if Λ(T) << (V/Ne)1/3 where Ne/V is the number density of electrons. For T = 4000 K and P/P 9. Show that the vibrational partition function of a harmonic oscillator
with respect to the level v = 0 is given by where ν is the oscillator frequency in cm -1
. Show that an additional term exp(-hcν/2kT) should be included
when isotope effects on the zero point energy are to be considered. Using the effects of zero point energy changes only, calculate the ratio K(H)/K(D), at 600 K, of the equilibrium constants of the gas phase reactions The vibration frequencies of HI and of H2 are
2300 and 4400 cm-1 respectively.
How would you expect the values of the partition functions to affect the value of K(H)/
K(D)? 10. (a) Starting from the realtionship between the translational energy of a particle inside a cubic container, show that the translational partition function is given by
and V = L3. (b) Consider N identical non-interacting particles moving in a constant volume V. Starting from basic statistical mechanical relationships for the internal energy, Helmholtz free energy amd entropy, show that the following relationships apply
(c) Explain why the expression for qtr is invalid for small values of L and estimate the dimension where the invalidity will become significant for oxygen molecules at 298 K.
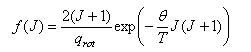
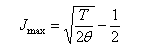
CD
4 in the cage. In the gas phase CD4
has two degenerate fundamental vibration bands close to 1000 cm
-1 and two close to 2000 cm-1
. Suggest an explanation for the observed value of the heat capacity
at 200 K and indicate the likely form of the heat capacity curve in the
temperature range 65 to 200 K.
Hence show that the heat capacity at constant volume is given by
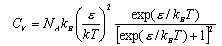
T/K
0.1
0.15
0.21
0.27
0.33
0.40
0.50
0.70
1.00
CV/J K-1mol
-1
5
11
17
22.5
23
20
18
12
8
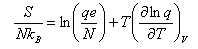
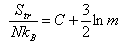
The standard molar entropy of Ne at T = 298 K is Smo = 146.2 J K−1 mol−1. Determine Smo for Ar at T = 298 K. Take the masses to be: Ne = 20, Ar = 40.
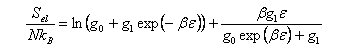
Obtain the limiting values of Sel for kBT << ε and kBT >> ε, and discuss the physical meaning of the results.
o = 210.5 J K−1mol−1. Explain how this information could be used to estimate the bond length of NO, indicating any assumptions made.
T/K
10
20
30
40
50
61.5
CP/T(J K-1
mol-1)
0.29
0.71
0.82
0.85
0.88
0.97