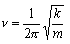
The basic topics to cover are:
(i) The vibrational energy levels and wavefunctions of a simple harmonic oscillator. The shape of the potential energy curve. The characterization of the potential energy curve in terms of dissociation energy, force constant, etc. The Franck-Condon principle. Zero point energy. The effects of anharmonicity on the spacing of the levels.
(ii) The population of vibrational levels as a function of temperature. Contributions of vibration to the heat capacities of gases (it will be useful for you to refer to your first year work on heat capacities).
(iii) The vibrations of simple polyatomic molecules. Normal modes. Consider the vibrations of a triatomic molecule, e.g. CO2 , in detail. The idea that vibrational modes must obey symmetry rules, but without the detail of group theory. Selection rules for excitation of vibrational levels.
(iv) Infrared and Raman spectroscopy of simple polyatomic molecules, e.g. CO2, C2H2, N2O, BF3, ClF3, NF3. Some of the tools that are used to assign a particular vibration to a band in the spectrum, e.g. polarization/depolarization in Raman spectroscopy, PQR structure in infrared.
Almost any general book on spectroscopy will cover most of the topics above. There is an Oxford Chemistry Primer, Brown, Molecular Spectroscopy . Other suitable ones have been written by Whiffen, Banwell, Barrow, Hollis, Dixon. The books Molecular structure, and Chemical Consequences of Nuclear Spin, both by Wheatley, and very old, are useful for reading about structural determination, and bosons and fermions respectively.
Herzberg, Diatomic Molecules is more advanced but is extremely well written and is useful for reference, especially if you only read the sections in large print.
The applet below shows all the four vibrational modes of a linear symmetric triatomic and is useful for question 8. Press "Start" to set the vibrations in motion. The "frequency" slider should be used to adjust the speed of the motion so that it appears reasonably smooth (this will be computer dependent). The masses of the atoms can be adjusted over a wide range and, because this will also cause large frequency changes, you may need to adjust the "frequency" slider again. The three vibrational modes can be switched on and off by the buttons at the top. Switching them on and off allows you to examine the effects of masses on the different modes more clearly. The relative phase button also changes the phase of the in and out of plane bending motions. In certain positions, e.g. 90o and 180o the combination of the two degenerate bending vibrations generates a rotation about the molecular axis and, for these two angles the rotation is in opposite directions.
The normal modes in XY2 do not change character as the masses are varied, but the actual motions change enormously. Note that the central atom never moves in the symmetric stretch however light the central atom (this is required by symmetry) whereas the central atom does nearly all the moving in the antisymmetric stretch and bend when it is the light atom.Note also that the antisymmetric stretch is always the higher of the two stretching vibrations (this can be observed by watching the beating of the motions when the bend is switched off.
I have found that this applet is very sensitive to the computer it is on and the version of java being used. If you download it with the controlling html program (VibrationJ.html) there is some scope for altering the running parameter, in particular the "rest" parameter which controls how long the calculation pauses to allow the graphics time to catch up. Altering the size of the display will also have an effect (it is the graphics that is slow not the calculation).
The second applet shows how the vibrational sub-structure of an electronic transition varies with various parameters, principally the difference in bondlengths between ground and excited states and, to a lesser extent, the force constant and dissociation energies of the upper state (the parameters of the ground state being held fixed), i.e. it is concerned with the Franck-Condon principle (see question 3). The calculation of the intensities is based on the overlap integrals of the wavefunctions for a harmonic oscillator, also shown for selected states in the diagram. These are taken to be centred not on re, which would be strictly correct, but on the mid point of the motion at the appropriate potential energy. In this way some account is taken of the gradual lengthening of the mean bondlength by anharmonicity. The two potential energy curves are Morse functions but are calculated in terms of the dissociation energy and force constants rather than the usual pair of parameters (D and α). The value of v at which the molecule would dissociate is also given. There are some small numerical inaccuracies around the Δr = 0 point. This is because I felt it necessary to effect some economies in what is quite a large calculation.
Click here for information concerning applets.
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
(i) The potential energy, V, for a harmonic oscillator is given by
V = kx2/2
where k is the force constant and x is the displacement from equilibrium. Show by direct substitution that the wave-function
ψ = Aexp(-λx2)
where
λ = (mk/4h2)1/2
is a solution of the Schrodinger equation for a harmonic oscillator of mass m. Determine the corresponding energy, expressing your answer in terms of the vibrational frequency,
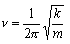
Explain why, for a diatomic molecule, the mass in the equation for the harmonic oscillator in question 1 must be replaced by the reduced mass.
Given that the stretching frequency of a C-C bond is approximately 1000
cm-1 calculate
(a) the stretching frequency of doubly and triply bound carbon atoms assuming
that the force constants are double and triple the single bond value respectively,
(b) the frequencies of a CH bond and of a Cl2 molecule on the
assumption that all single bond force constants are equal,
(c) the frequencies of the series HX where X is a halogen.
Look up the actual experimental values in each case, make a table of calculated and observed frequencies and comment on the similarities and differences between them.
(i) Use the wave function from question 1 to determine the position of maximum probability density for the harmonic oscillator wave-function in the vibrational ground state. How does the result compare (qualitatively) with the time averaged probability of finding a particle at a specific location in a classical harmonic oscillator?
The wave function for the v = 2 state is
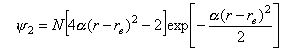
where α2 = 2π2mν2.
Plot the potential from question 1 and superimpose a plot of the square of the ν = 2 wavefunction. Compare the positions of the maxima with the positions of the classical turning points for a vibration with the same amount of energy.
(ii) The figure below shows a sequence of electronic transitions (photoelectron spectroscopy) from the v = 0 state in the H2 molecule to a sequence of vibrational states in the ground state of the H2+ ion. Using the results from part (i) as a guide, explain, with the aid of a diagram, the factors responsible for the variations in peak intensity and peak separation.
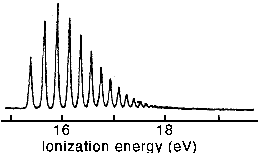
(iii) The harmonic oscillator becomes a less good approximation for vibrational energies at higher energies and, instead of being equally spaced, the levels converge. The peak positions (cm-1) in (ii) are well represented by the equation Tv = 123506 + Ev where Ev = 2322(v + 1/2) - 66.2(v + 1/2)2. Given that the spacing between successive vibrational peaks will converge to zero at the dissociation limit, estimate the dissociation energy of H2+. Why does the spacing converge to zero at the dissociation limit?
(iv) The convergence of the vibrational levels at high n can be accounted for by an anharmonic potential such as the Morse potential
V = De{1 - exp[-α(r - r e)]}2
where α is a constant (equal to 1.48 x 1010 m−1 in this case) and D is the dissociation energy. Plot the Morse potential and superimpose a sketch of the potential for a harmonic oscillator.
The turning points of classical vibrational motion in the Morse potential at fixed energy Ev can be obtained by rearranging the above equation and are given by
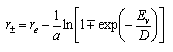
From the figure in (ii) the most probable transition is the one for which the overlap of ground and excited state wavefunctions is a maximum (n = 2 ). Use the equation above to calculate the turning points for an energy corresponding to this n = 2 state. Then, by assuming that the maximum overlap between ground and excited states occurs at the same r as the classical turning points, use your values of the turning points to calculate re for H2+. (The equilibrium bond length for H2 is re = 0.741 x 10-10 nm.)
(i) Why do atomic masses affect vibrational zero point energies of diatomic molecules? How can the zero point energy influence the rates of chemical reactions?
(ii) During the oxidation of benzaldehyde by permanganate in solution a CH(CD) bond is broken. By considering the change in zero point energies of the reactants alone, estimate the maximum ratio kH/kD of the rate constants. The vibration frequency of the CH bond is about 2900 cm-1 and you may neglect any isotopic effect on the pre-exponential term in the expression for the rate constant. What happens if the zero point energies in the transition state for the reaction cannot be neglected?
By calculating the contribution of zero point energy to the enthalpy of the reaction, calculate its effect on the ratio K(H)/K(D), at 600 K, of the equilibrium constants of the gas phase reactions
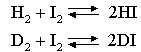
The vibration frequencies of HI and of H2 are 2300 and 4400 cm-1 respectively and the atomic weight of iodine is 127.
The frequency of the stretching vibration of CO is 2200 cm-1. In the infrared emission spectrum of the first overtone (v = 2 → 0) of CO formed in an oxy-acetylene flame a series of transitions corresponding to v = 3 → 1, 4 → 2, etc. are observed. These have slightly different frequencies because of anharmonicity (as explained in question 3). The intensities of the transitions depend on the populations of the v = 2, 3, 4, etc. levels and are proportional to
I = (v + 1)(v + 2)exp[-(v + 2)hcν/kBT]
where v refers to the lower level in each transition. Values of the intensity are
| I | 4.0 | 5.9 | 5.5 | 4.6 | 3.9 | 3.2 |
| v | 0 | 1 | 2 | 3 | 4 | 5 |
Use a graphical method to determine the temperature of the flame.
Use the following data for O2 to plot a graph of the heat capacity, CV, as a function of temperature. Discuss the shape of this graph and the origin of the temperature variation in terms of the properties of the O2 molecule. To what extent is the form of the function applicable to other molecules? (You will find it very helpful to refer to 1st year tutorial on heat capacities .)
| T/K | 200 | 300 | 500 | 1000 | 1500 |
| CV/R | 2.503 | 2.533 | 2.739 | 3.197 | 3.399 |
The molecule O2 has a vibrational frequency of 1553 cm-1. Use the method of question 2 to use this frequency to estimate the vibration frequencies of F2, Cl2, Br2 and N2. Then use the heat capacity curve for O2 to estimate C V for each of the four species at 500 K.
It is important to understand the meaning of some of the symmetry operations that are used to classify the symmetry of molecules, e.g. axes of symmetry, planes of symmetry, centres of inversion. You can do this without doing group theory.
The following are some simple rules to follow when assessing the vibrational modes of molecules.
(i) The number of vibrational modes is 3N − 6 if the molecule is non-linear and 3N − 5 if it is linear.
(ii) The number of stretching modes is equal to the number of bonds between pairs of atoms (all types of bond (single, double, triple) count as one bond). All remaining vibrations must be bends of some kind.
(iii) For a molecule with an axis of symmetry the change in dipole accompanying a vibration can be parallel to the axis or perpendicular. If the symmetry axis is 3-fold or higher, perpendicular vibrations (i.e. vibrations where the dipole moment change is at rightangles to the principal axis of symmetry) will be degenerate, i.e. vibrational modes will occur in pairs each with an identical frequency.
(iv) Stretching vibrations occur at higher frequencies than bending ones (it is easier to bend something than to stretch it). Antisymmetric stretching vibrations occur at higher frequencies than symmetric ones.
8. (a) Describe the normal modes of vibration of a linear symmetrical
XY2 molecule and deduce, in terms of dipole moment
and polarisablility changes, which of the modes are infrared and/or Raman
active. How are the selection rules modified if the molecule is linear but
unsymmetric, of the type XYY or XYZ?
(b) Assign the three fundamental vibration frequencies of the linear N
2O molecule given below. All three bands are infrared active and information about the Raman spectrum is given in the table.
| Frequency/cm-1 | 2223.5 | 1285.0 | 588.8 |
| Raman | polarized | polarized | absent |
In the region associated with the stretching modes of a trifluoride molecule XF3, the infrared and Raman spectra of the vapour exhibit bands with the following wavenumber (cm -1):
| Raman | Raman | Infrared | Infrared |
| 675 | strong, polarized | 675 | strong |
| 612 | weak, depolarized | 614 | very strong |
| 552 | strong, polarized | 552 | weak |
Sketch and assign the vibrations associated with the observed frequencies.