(i) Review quantum mechanics, especially ideas about angular momentum.
(ii) Alkali metal spectra. Penetration and shielding, the quantum defect.
(iii) Helium. Singlets and triplets. Spin wavefunctions. Exchange and Coulomb integrals. The helium-neon laser.
(iv) Many electron atoms, Russell-Saunders coupling, Hund's rules.
(v) Normal and anomalous Zeeman effects.
(vi) Revise and extend your knowledge of elementary molecular orbital theory, which is essential for understanding the order and assignment of electronic energy levels.
(vii) Selection rules for electronic transitions. Transition moments. The Franck-Condon principle, its application to diatomic and polyatomic molecules.
(viii) The determination of the dissociation energy of a diatomic molecule.
(ix) Photoelectron spectroscopy.
For atomic spectra the most suitable books are the OUP Primers Atomic Spectroscopy by Softley and Atomic Spectra by Richards & Scott, but you ought also to use Molecular Quantum Mechanics by Atkins and Friedman, Chapter 7. You will also find it useful to revise the first year atomic spectra, which has been extensively revised since you did it. For the molecular electronic spectroscopy and valence almost any general book on spectroscopy will cover most of the topics. Suitable ones have been written by Banwell and Hollis. There is a book on Valence by Murrell, Kettle, Tedder. Photoelectron spectroscopy is covered in Photoelectron Spectroscopy by Eland. Electronic Spectra by Herzberg is more advanced but is extremely well written and is a useful reference book, especially for molecular orbital theory, for examples of electronic transitions, and for answering the questions that no-one else does.
The Photoelectron Spectroscopy experiment is a must. There are also good experiments on the dissociation of iodine and the electronic spectrum of nitrogen.
Where the question number is enclosed in a button, e.g. , you can obtain help or comments about the question by clicking it.
1. You should make sure that you are proficient in the test, which you start by clicking the button below. You will not be able to obtain the answers to the other questions until you have scored better than 75%!.
Wavenumbers of some of the transitions in (i) the emission spectrum of atomic hydrogen (one line is missing) and (ii) the absorption spectrum of an unknown hydrogenic ion (e.g. He+, Li2+ , etc.) are
| (i) Hydrogen (cm-1) | 5500.8 | 4616.5 | 3808.2 | 2467.8 |
| (ii) Unknown ion (cm-1) | 1719865 | 1706927 | 1685468 | 1645965 |
(a) Identify the principal quantum numbers for the upper and lower states for each of the transitions listed in (i) (without using the literature value for the Rydberg constant, R) and determine a value for R H of atomic hydrogen.
(b) Suggest an identification of the unknown ion and assign the transitions in (ii). Derive a value of RX for this ion and verify that the ratio RX/R H is in agreement with that predicted from the reduced masses on the basis of your identification (me = 5.486 x 10 -4 amu).
(a) The applet (click here for information concerning applets; the filenames here are tutorials/electronic/atomic/atomic.jar and tutorials/electronic/atomic/AtSpectraAppletJ.html). In the emission spectrum of sodium (shown below; if the quality is poor try pressing Refresh in the View menu) two series of multiplets can be identified at the following wavelengths (nm):
| Series I (nm) | 1140 | 619 | 515 | 475 |
| Series II (nm) | 820 | 569 | 498 | 467 |
Show that they terminate in a common level and estimate the ionization energy from that level. The transition at 8769 cm-1 is a doublet of separation 17 cm-1. The lowest frequency absorption line is a doublet with a mean frequency of 16970 cm-1 and the same separation of 17 cm-1 (the yellow doublet in the spectra above, often called the sodium D lines). Sketch and label the energy level diagram.
The sodium D lines are shown on an expanded scale in the upper of the two spectra below (if the quality is poor try pressing Refresh in the View menu). The lower spectrum shows the effect of a magnetic field on the doublet structure. Explain this effect.
Explain the following.
(a) The four lowest energy electronically excited states of He, as determined at low energy resolution, lie at 159850, 166271, 169083 and 171129 cm -1 above the ground state. The absorption spectrum of He displays a strong line only at one of these energies.
(b) He gas shows negligible absorption of radiation in the infrared region of the electromagnetic spectrum, but strong absorption bands are seen at 4858 and 9233 cm-1 when the gas is excited in an electrical discharge. If Ne is added to the He electrical discharge, the intensity of these absorption bands diminishes and light is emitted at 15803 cm -1 (632.8 nm).
5. The He I photoelectron spectra of Ar, Kr, and Xe each contain two lines at the ionization energies given below.
| Element | I.p./eV | I.p./eV |
| Ar | 15.759 | 15.937 |
| Kr | 14.000 | 14.665 |
| Xe | 12.130 | 13.436 |
6. Construct a molecular orbital energy level diagram appropriate to diatomic molecules formed from elements from Li to Ne, and explain the factors which cause some atomic orbitals to couple efficiently and some not.
Account for the following observations:
(a) The term symbols for the electronic ground states of Si2 and C2 are 3Σg− and 1Σg+ respectively.
(b) The lowest two electronic states of S2 have term symbols 3Σg− and 1Δg; they are separated by about 4000 cm-1 and have very similar rotational constants.
(c) The highest kinetic energy peak in the photoelectron spectrum of O2 consists of a progression of lines separated by about 1700 cm-1, whereas that of N2 consists of a strong line and a short progression with one or two weak lines. The ground state vibrational frequency of O2 is 1550 cm−1.
(d) The dissociation energy of Mg2 is only 800 cm-1.
(e) The first excited state of NO lies only 121 cm−1 above the ground state.
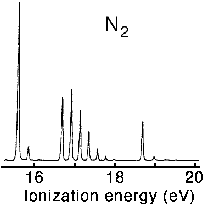
7. Interpret the photoelectron spectrum of N 2 shown in the figure below using molecular orbital theory for homonuclear diatomics and the Frank-Condon principle. The adiabatic ionization potentials for nitrogen are 15.58, 16.69, and 18.76 eV respectively.
A self consistent field calculation together with Koopman's theorem gives 17.36, 17.10 and 20.92 eV respectively. Comment on the differences.
8. The first band in the photoelectron spectrum of each of the halogens is shown in the upper of the two figures below. The whole spectrum in the range up to 21 eV is shown in the lower figure and some quantitative data relevant to the spectra are given in the table.
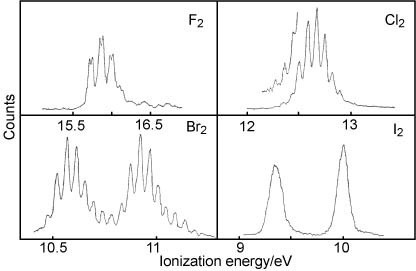
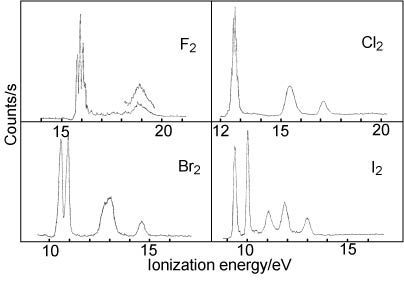
| Halogen | Ionization pot./eV | Vibration frequency/cm−1 | Change in bondlength/Å |
| F2 | 15.7 | 1065(894) | -0.10 |
| F2 | 18.4 | 500 | +0.32 |
| Cl2 | 11.5 | 645(557) | -0.10 |
| Cl2 | 14.0 | 323 | +0.37 |
| Br2 | 10.5 | 355(321) | -0.09 |
| Br2 | 12.4 | 187 | +0.35 |
| Br2 | 14.3 | Not resolved | Not determined |
| I2 | 9.2 | 236(214) | -0.08 |
| I2 | 10.7 | 125 | +0.26 |
| I2 | 12.7 | Not resolved | Not determined |
(i) Draw the molecular orbital diagram for the halogens and use it to assign the ionization potentials in the spectra.
(ii) Show that the changes in vibration frequency and bondlength on ionization are consistent with your assignment for each of the bands.
(iii) Show that the spin orbit coupling in the ions is also consistent with your assigment (use the values of the different spin-orbit coupling constants for the halogens from the quiz.
(iv) On the basis of your discussion in (ii) and (iii) account for the differing appearances of the band(s) associated with the first ionization.
The following band origins were derived from the electronic absorption spectrum of O2:
| v/ | 16 | 17 | 18 | 19 |
| v// | 0 | 0 | 0 | 0 |
| ν/cm−1 | 56719.5 | 56852.4 | 56954.5 | 57030.2 |
Analysis of the emission spectrum of the O atom reveals excited levels at 15867.7 and 33792.4 cm−1 above the ground state. Derive estimates for the ground state dissociation energy of O2. Explain how any ambiguities could be resolved by further experiments.
10.(a) What is a molecular orbital (MO)? What is the physical justification for approximating a MO as a linear combination of atomic orbitals?
(b) Outline the essential approximations that underlie Huckel theory for the p-electrons of conjugated organic molecules.
(c) Write down the secular equations for the cyclopropenium ion C3H3+ within Huckel theory, and obtain the corresponding energies in terms of the Coulomb integral (α) and resonance integral (β).
[You may find it helpful to note that x3 - 3x + 2 = (x - 1)[x(x + 1) - 2]]
(d) Determine the MO coefficients of the carbon atom 2p-orbitals for the lowest energy MO.
(e) For a closed-shell species, the p-electron charge on carbon atom i is defined by
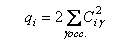
where the MOs are labelled by γ Ciγ is the MO coefficient on atom i, and the sum is over all occupied MOs.
(f) Determine qi for the carbon atoms in C3H3+. Suggest how this result might be rationalized in terms of valence-bond structures for the cation.
(a) Draw a molecular orbital energy level diagram of the O2 molecule and use it to show that the first band in the photoelectron spectrum gives rise to the electronic transition
O2(3Σg−) + hv → O2+(2Πg) + e−
(b) This electronic band exhibits a vibrational progression with a vibrational spacing of v = 1900 cm−1. Draw potential energy curves to illustrate the origin of this progression and discuss the physical principles involved.
(c) For sufficiently small displacements from its equilibrium bond length re/, the electronic potential energy curve V(r) of O2+(2Πg) can be approximated by that of a harmonic oscillator:
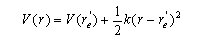
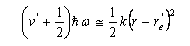
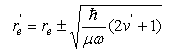
(d) Given that the most intense line in the observed spectrum has v/ = 1, and that the equilibrium bond length of O2(3Σg−) is re = 0.1208 nm, estimate re/. (e) Discuss whether or not the electronic process in part (a) obeys the usual electric dipole selection rules for an electronic transition in a linear molecule.