The reflection of neutrons (neutron reflectometry) at a surface is very similar to the better known phenomenon of the reflection of light (optical reflectometry). Here we use two animated simulations of the reflection of light (in the form of Java applets) to explain the main features of neutron reflection. We then use a further simulation to show how the important technique of contrast variation in neutron reflectometry can be usefully applied.
That a beam of neutrons can be reflected from a flat surface just like light was first demonstrated by Fermi but, until relatively recently, no-one had thought of following up the analogy with light and using a neutron beam to study thin films. Light reflected from a thin film may undergo strong interference depending on the wavelength of the light, its state of polarisation, the thickness of the layer and the refractive indices of the media involved. These effects can be explored using the applet displayed below (click here for information concerning applets; the filenames here are techniques/reflectivity/reflectivity.jar and techniques/reflectivity/ReflectivityAppletJ.html). The diagram represents an exact calculation of the light reflected at a layered surface. The left hand panel of the diagram shows the path of the beam as it is reflected from the thin layer and the inset shows in detail how the beam is partially reflected and transmitted at the two interfaces (the intensity of the partially reflected beams in the inset has been progressively multiplied up as the signal gets weaker in order to make the subsidiary beams visible).The middle panel shows the intensity observed as a function of angle, and the right hand panel shows the complete intensity pattern that would be obtained if the intensity were recorded over the whole angular range. The intensity is plotted on a log scale.
The following indicate some of the phenomena associated with reflectivity experiments that can be explored with this diagram.
(i) The fringe pattern is clear in the initial set-up of the diagram. The destructive interferences show as black bands in the panel on the right. For a given angle of reflection and a given thickness of the layer the path difference between beams reflected at the upper and lower interfaces is constant. This means that the number of occurrences of destructive interference in the angular range shown will increase as the wavelength of the light decreases. This can be demonstrated by varying the wavelength of the light (the range is from blue at 400 nm to red at about 650 nm).
(ii) Increasing the thickness of the layer increases the path difference in the two partially reflected beams and again generates more closely spaced fringes. The implication is that the much shorter wavelengths of x-rays and neutrons in comparison with light will mean that they can explore much thinner layers (of the order of molecular dimensions).
(iii) Variation of the refractive index (η) of the underlying medium so that it is identical with that of the layer causes the fringe pattern to disappear. The refractive indices of the incident medium and layer are respectively 1.0 and 1.333 so this condition occurs when η for the sub-phase is 1.333. As can be seen from the beams in the inset, there is no reflection from the lower surface at this point and hence no fringes. This use of "contrast matching" is very important in neutron reflection.
(iv) For electromagnetic radiation the state of polarisation affects the reflectivity, as can also be tested on the diagram. For neutron reflection the reflectivity follows the same equations as for light polarised perpendicular to the plane of reflection.
(v) Finally, in white light the reflectivity pattern is more complex because the interference is wavelength dependent. At each angle there is a superposition of the different strength signals from the different wavelengths. Resolution of the signal at a given angle into its different wavelengths therefore gives some information about the thickness of the layer. In practice, the range of wavelengths in visible light is not large enough to make this a useful procedure for exploring the thickness of a thin film. However, it is a commonly used method in neutron reflection, where the spread of wavelengths may cover an order of magnitude.
The applet below is much closer to a real experiment. It shows the phenomenon of Newton's rings from a thin polymer layer formed by spin coating on to silicon. The colour and interfrence pattern gives a useful and rapid means of measuring the uniformity and thickness of the polymer film down to about 100 nm. The interference of light is governed by the same principles as for the first applet. However, here the angle of incidence is fixed at 90o. Fringes are only observed if there is a variation of thickness across the film. A quadratic variation of thickness has been assumed and the thicknesses at the centre and at the rim of the sample can be adjusted. Since such films would normally be observed in white light the simulation is set to start in white light. Because intensities and colours vary from display to display these can be adjusted by the two sliders on the right using the disc on the left for calibration. The disc on the left represents light reflected from a surface with no polymer, i.e. no interference. Although no interference fringes are observed from the right hand disc when the layer is set to be of uniform thickness, there may still be wavelengths where there is strong constructive or destructive interference (these can be explored directly with the applet, click here for information concerning applets; the filenames here are techniques/newtonsRingsSi/newtonsRingsSi.jar and techniques/newtonsRingsSi/NewtonsRingsAppletJ.html). The colour of the right hand disc should therefore never be white for the range of accessible parameters in the applet. The display on this applet is very demanding and may be slow on older computers.
There are two obvious advantages of doing similar experiments with neutrons; the wavelengths of neutrons are much shorter than those of light and so thinner films can be studied, and the refractive index for neutrons is related in quite a simple way to the composition of a material. Neutron reflection could therefore give information about the structure and composition of films of thickness of the order of molecular dimensions. Surfactants, polymers, proteins all have dimensions suitable for investigation by this means.
The key feature that makes neutron reflection a very powerful technique for investigating molecular films is that neutrons are scattered differently by H and D nuclei and this leads to the powerful method of contrast variation, which is illustrated in the applet below (click here for information concerning applets; the filenames here are techniques/contrast/contrast.jar and techniques/contrast/contrastAppletJ.html). The left hand side of the diagram plots the reflectivity as a function of momentum transfer. The reflectivity is again plotted on a log scale because it falls off very rapidly with angle (this is because neutron refractive indices are all very close to unity and the differences between them are very small). The use of momentum transfer (defined as (4πsinθ)/λ) makes it possible to integrate the effects of reflection angle and wavelength into a single parameter. The range of reflectivity shown corresponds to the typical experimentally accessible range after subtraction of the background. The right hand side of the diagram uses a colour code for the neutron scattering length density (this is a more convenient quantity than refractive index for neutrons). Red corresponds to a typical fully deuterated hydrocarbon material (scattering length density 6.5 x 10−4 nm−2) and blue to a fully protonated one (-0.6 x 10−4 nm−2). These represent the two limits normally encountered and most other materials fall in between. The colour used for these intermediate materials is the appropriate arithmetical combination of red and blue. Air has a scattering length density close to that of H2O and is therefore coloured blue. For an air/water experiment the neutron beam is incident on the air side, as shown. Initially the scattering length densities are set for a deuterated, but not very dense monolayer at the air/D2O interface. The coarse divisions on the sliders do not always allow exact matching of the different substrates. The following will illustrate some of the possibilities for varying the contrast.
(i) Decrease the scattering length density of the water until it approximately matches that of air. At this contrast the reflectivity is generated only by the layer so that if either the thickness of the layer is reduced to zero or its scattering length density is adjusted to that of air the reflectivity will become zero. This contrast condition is referred to as null reflecting and the water is often called null reflecting water (NRW). Neutron reflectometry becomes truly surface selective under these conditions.
(ii) With the scattering length density of water set to 0, i.e. NRW (about 90% H2O and 10% D2O), set the scattering length density of the layer to a value that gives a significant reflected intensity. Then increase the thickness of the layer until a destructive fringe is observed. Now vary the scattering length density of the layer and note that the position of the fringe is not changed. This illustrates that, for layers above about 3 nm, thickness and composition of a layer may be determined independently of each other. As the thickness of the layer decreases below about 2.5 nm this separation becomes increasingly difficult at this contrast.
(iii) With the contrast still at zero set the layer thickness to about 3.5 nm. Now increase the scattering length density of the water up to that of D2O. The phase of the scattering at the layer/D2O boundary chnages so that the destructive fringe becomes a constructive one and the minimum moves to lower momentum transfer. Thus the resolution of composition and thickness is more sensitive when D2O is the sub-phase.
(iv) With the conditions set approximately as in (iii) vary the scattering length density over its whole range. You will see that the interference fringe is strongest when the scattering length density of the layer is intermediate between that of air and D2O. It is also possible to obtain the same reflectivity profile for two completely different settings of the layer scattering length density. This is a manifestation of the phase problem (the reflectivity is determined by the square of the amplitude of the reflected wave and these two conditions have the same intensity but amplitudes of opposite phase).
(v) The experiment is not limited to the air/water interface. Pressing the button at the bottom of the diagram allows you to examine the contrast conditions for three other solid media, silicon, quartz and sapphire. In principle, any solid that is transparent to neutrons can be used but, so far, these are the only three that have been used. The conditions (i) to (iv) above all also apply to the interfaces of any of these three solids with water. However, there is one important new feature and that is that a good contrast between layer and surroundings can now be obtained with a fully protonated layer, especially using sapphire. This cannot be done at the air/water interface.
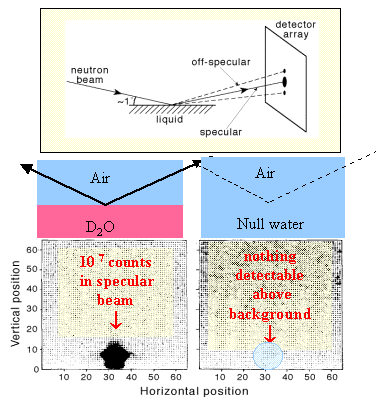
The diagram above makes it clear that it is possible to vary the contrast so that there is no signal from the clean surface. The reflection from D2O and NRW, the appropriate experimental set-up, and the signal observed on a square multidetector are shown below. The specular peak falls near the bottom of the detector, mid-way across. The remaining off-specular signal is background scattering.

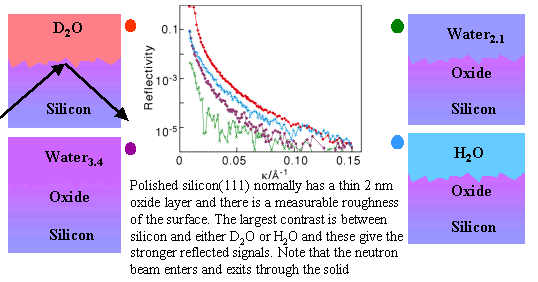
The large variation of reflectivity with H/D composition of water is also shown at the clean silicon/water interface in the next figure. At the silicon/water interface there are the additional complexities of roughness and the presence of an oxide layer but the characteristics of both can be determined by combining the information from the different water contrasts.
The method of contrast variation is the key to the effective utilization of neutron reflection. For example, it may be used to highlight one component in an interfacial system containing two or more components. This makes it possible to investigate interfacial layers that would be too complex for other techniques. Contrast variation is used in more or less the same way in Neutron Small Angle Scattering
To see contrast variation in practice go to Neutron Reflection at the Air/Water Interface or Neutron Reflection at the Solid/Water Interface. Further examples will be found in Surfactant Mixtures and Polymer/Surfactant mixtures.